题目内容
18．
已知△CDE是△CAB经相似变换后得到的像，且∠A=30°，∠CDE=30°，AB=4，DE=2，AC=3，则CD=1.5．
分析 由△CDE是△CAB经相似变换后得到的像得到两三角形相似，利用相似得比例求出CD的长即可．
解答 解：由题意得：△CDE∽△CAB，∠A=30°，∠CDE=30°
∵AB=4，DE=2，AC=3，
∴$\frac{DE}{AB}$=$\frac{CD}{AC}$，即$\frac{2}{4}$=$\frac{CD}{3}$，
解得：CD=1.5，
故答案为：1.5
点评 此题考查了相似三角形的性质，熟练掌握相似三角形的性质是解本题的关键．
练习册系列答案
相关题目
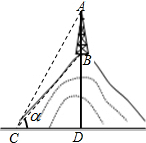如图，在铅直高度为200m的小山上建有一座电视转播塔，某数学兴趣小组为测量电视转播塔的高度，在山脚的C处测得山顶B的仰角为30°（即∠BCD=30°），测得塔顶的仰角为45°（即∠ACD=45°），请根据以上数据求塔高AB．（精确到1m．备用数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．
13．
如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为（-1，0），半径为1．若D是⊙O上的一个动点，线段DA与y轴交于点E，则△ABE面积的最大值为（ ）
如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为（-1，0），半径为1．若D是⊙O上的一个动点，线段DA与y轴交于点E，则△ABE面积的最大值为（ ）| A． | 2+$\sqrt{2}$ | B． | 2+$\frac{\sqrt{2}}{2}$ | C． | 1 | D． | 2 |
某服装专卖店老板对第一季度男、女服装的销售收入进行统计，并绘制了扇形统计图（如图）．由于三月份展开促销活动，男女服装的销售收入分别比二月份增长了40%，64%，已知第一季度男女服装的销售总收入为20万元．