题目内容
5. 如图所示,已知平行四边形ABCD和平行四边形EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.
如图所示,已知平行四边形ABCD和平行四边形EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.
分析 由E、F是?ABCD的对角线AC上两点,DF∥BE.易证得AB=CD,∠BAE=∠CDF,∠AEB=∠CFD,则可证得△ABE≌△CDF,继而证得结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF,
又∵∠DF∥BE,
∴∠BEF=∠DFE,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠AEB=∠CFD}\\{∠BAE=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(AAS).
∴AE=CF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{x-2>0}\\{\frac{x}{2}≤4}\end{array}\right.$的解集是( )
| A. | x≥8 | B. | x>2 | C. | 0<x<2 | D. | 2<x≤8 |
13.下列说法正确的有( )个
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.解方程:$\frac{x}{3}=1-\frac{x-1}{4}$去分母后正确的是( )
| A. | 4x=1-3(x-1) | B. | x=1-(x-1) | C. | 4x=3-(x-1) | D. | 4x=12-3(x-1) |
17.已知两直线y1=kx+k-1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是$\frac{2013}{4028}$.
15. 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )
 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )| A. | x<-2 | B. | x≤-2 | C. | x>-2 | D. | x≥-2 |
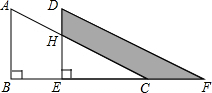 如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积48.
如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分的面积48.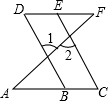 如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?
如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?