题目内容
1.已知正实数a,b满足a-b=4,ab=21,则a2+b2=58,$\frac{1}{a}$+$\frac{1}{b}$=$\frac{10}{21}$.分析 先根据a-b=4得出(a-b)2及a+b的值,代入代数式进行计算即可.
解答 解:∵a-b=4,ab=21,
∴(a-b)2=a2+b2-2ab=16,
∴a2+b2=16+2ab=16+42=58,
∴a+b=$\sqrt{(a+b)^{2}}$=$\sqrt{{(a-b)}^{2}+4ab}$=$\sqrt{16+84}$=10,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{10}{21}$.
故答案为:58,$\frac{10}{21}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
12.数轴上表示无理数$\sqrt{28}$的点界于哪两个相邻的整数点之间( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 5和6 |
16.某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式y=8.1x.
| 数量x(千克) | 2 | 3 | 4 | 5 |
| 售价y(元) | 16.2 | 24.3 | 32.4 | 40.5 |
13.如果(m-3)m=1,那么m应取( )
| A. | m≥3 | B. | m=0 | C. | m=3 | D. | m=0,4或2 |
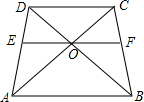 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.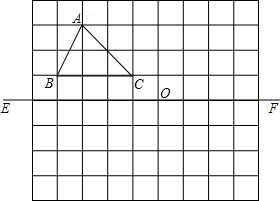 如图的小方格都是边长为1个单位的正方形,按照下列要去作图,(不写作法,只作出图形即可)
如图的小方格都是边长为1个单位的正方形,按照下列要去作图,(不写作法,只作出图形即可)