题目内容
2.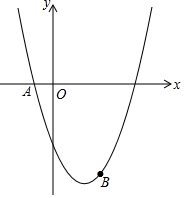 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).(1)求该二次函数的表达式;
(2)用配方法求该抛物线的对称轴及顶点坐标;
(3)点C(m,m)与点D均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值;
(4)在(3)的条件下,试问在该抛物线的对称轴上是否存在一点P,使PC+PB的值最小,若存在求出点P的坐标;若不存在,请说明理由.
分析 (1)由条件可知点A和点B的坐标,代入解析式可得到关于a和c的二元一次方程组,解得a和c,可写出二次函数解析式;
(2)利用对称轴为x=-$\frac{b}{2a}$,顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)计算出其顶点坐标即可;
(3)把点的坐标代入可求得m的值.
(4)存在.如图,由(2)可知C(6,6),作点B关于对称轴的对称点B′(1,-9),连接CB′与对称轴的交点即为所求的点P.求出直线CB′的解析式即可解决问题.
解答 解:(1)将A(-1,-1),B(3,-9)代入,
得$\left\{\begin{array}{l}{a+4+c=-1}\\{9a-12+c=-9}\end{array}\right.$,
∴a=1,c=-6,
∴y=x2-4x-6;
(2)∵-$\frac{b}{2a}$=-$\frac{-4}{2}$=2,$\frac{4ac-{b}^{2}}{4a}$=$\frac{-24-16}{4}$=-10,
∴对称轴:直线x=2,顶点坐标:(2,-10);
(3)∵点P(m,m)在函数图象上,
∴m2-4m-6=m,
∴m=6或-1.
∵m>0,
∴m=6.
(3)存在.如图,由(2)可知C(6,6),作点B关于对称轴的对称点B′(1,-9),连接CB′与对称轴的交点即为所求的点P.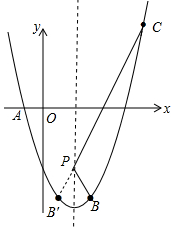
设直线CB′的解析式为y=kx+b,把A、B代入得到$\left\{\begin{array}{l}{6k+b=6}\\{k+b=-9}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=-12}\end{array}\right.$,
∴直线CB′的解析式为y=3x-12,
∴P(2,-6).
∴当点P坐标为(2,-6)时,PB+PC最小.
点评 本题考查二次函数综合题、一次函数、待定系数法、最短问题等知识,解题的关键是灵活运用所学知识解决问题,学会利用对称解决最值问题,属于中考压轴题.

 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )| A. | abc>0 | B. | a+b+c<0 | C. | b<a+c | D. | 4a+2b+c>0 |
 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:| R | … | 2 | 4 | 8 | 10 | 16 | … |
| I | … | 16 | 8 | 4 | 3.2 | 2 | … |
 如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.
如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.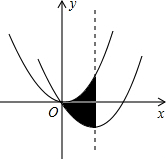 如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.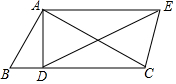 如图三角板ABC中,∠BAC=90°,∠B=60°,把△ABC绕点A逆时针旋转30°得到△ADE,连接CE,则∠CED=45°.
如图三角板ABC中,∠BAC=90°,∠B=60°,把△ABC绕点A逆时针旋转30°得到△ADE,连接CE,则∠CED=45°.