题目内容
4.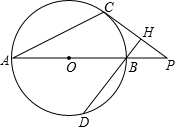 如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.
如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.(1)求证:PC是⊙O的切线;
(2)若sin∠P=$\frac{2}{3}$,求$\frac{BH}{BD}$的值.
分析 (1)连接OC,根据等腰三角形的性质得到∠PAC=∠OCA,推出∠COP=∠OBH,得到OC∥BH,于是得到结论;
(2)设⊙O的半径为2a,解直角三角形得到OP=3a,PB=OP-OB=a,作OG⊥DH,根据相似三角形的性质即可得到结论.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠PAC=∠OCA,
∴∠COP=∠PAC+∠OCA=2∠PAC,
∵∠PBH=2∠PAC,
∴∠COP=∠OBH,
∴OC∥BH,
∵BH⊥CP,
∴OC⊥CP,
∴PC是⊙O的切线;
(2)解:设⊙O的半径为2a,
在Rt△OCP中,sin∠P=$\frac{2}{3}$,OC⊥CP,
∴OP=3a,
∴PB=OP-OB=a,
作OG⊥DH,
则BG=$\frac{1}{2}$BD,△OBG∽△PBH,
∴$\frac{BH}{BG}=\frac{BP}{OB}=\frac{1}{2}$,
∴$\frac{BH}{BD}=\frac{1}{4}$.
点评 本题考查了相似三角形的判定和性质,切线判定,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
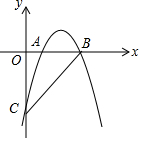 已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.