题目内容
8.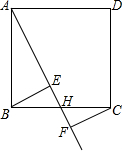 如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是BE∥CF.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
分析 (1)当BE∥CF时,△BEH≌△CFH.根据AAS即可判断.
(2)结论:当BH=EH时,四边形BFCE是矩形.根据矩形的判定方法即可判断.
解答 解:(1)当BE∥CF时,△BEH≌△CFH.
理由:∵BE∥CF,
∴∠BEH=∠CFH,
在△BEH和△CFH中,
$\left\{\begin{array}{l}{∠BEH=∠CFH}\\{∠BHE=∠CHF}\\{BH=CH}\end{array}\right.$,
∴△BEH≌△CFH(AAS).
故答案为BE∥CF.(答案不唯一).
(2)结论:当BH=EH时,四边形BFCE是矩形.
理由:∵BH=CH,EH=FH,
∴四边形BFCE是平行四边形(对角线互相平分的四边形为平行四边形),
∵当BH=EH时,则BC=EF,
∴平行四边形BFCE为矩形(对角线相等的平行四边形为矩形).
点评 本题考查正方形的性质、全等三角形的判定和性质、矩形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
16.将长度为6cm的线段向上平移8cm再向右平移6cm,所得线段长为( )
| A. | 12cm | B. | 10cm | C. | 6cm | D. | 无法确定 |
13.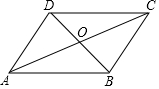 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
 如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )
如图,已知AC、BD相交于点O,AO=CO,BO=DO,则图中能判定全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
18.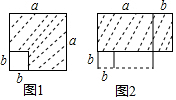 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab 十b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)═a2+ab-2b2 |
 如图,已知在矩形ABCD中,AB=2a,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,△ABE是等边三角形.
如图,已知在矩形ABCD中,AB=2a,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,△ABE是等边三角形.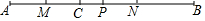 如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:
如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求: