题目内容
17.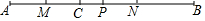 如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:
如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:(1)线段AM的长;
(2)线段PN的长.
分析 (1)根据线段中点的性质计算即可;
(2)结合图形、根据线段中点的性质计算.
解答 解:(1)∵M为AC中点,
∴AM=$\frac{1}{2}$AC=$\frac{3}{2}$cm;
(2)∵AP=AC+CP,CP=1cm,
∴AP=4cm,
∵P为AB的中点,
∴线段AB=2AP=8 cm,
∵CB=AB-AC,AC=3cm,
∴线段CB=5cm,
∵N为CB的中点,
∴CN=$\frac{1}{2}$BC=$\frac{5}{2}$cm,
∴PN=CN-CP=$\frac{3}{2}$cm,
答:(1)线段AM的长为$\frac{3}{2}$cm,(2)线段PN的长为$\frac{3}{2}$cm.
点评 本题考查的是两点间的距离的计算,掌握线段的中点的性质、灵活运用数形结合思想是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
2.若$\sqrt{1-2n}$+$\sqrt{2n-1}$有意义,则(-n)2的平方根是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $±\frac{1}{4}$ | D. | $±\frac{1}{2}$ |
7. 如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
 如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )| A. | 100° | B. | 65° | C. | 75° | D. | 105° |
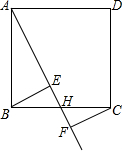 如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.