题目内容
20.解下列不等式(组):(1)$\left\{\begin{array}{l}{\frac{1+2x}{3}>x-1}\\{4(x-1)<3x-4}\end{array}\right.$
(2)$\frac{1-2x}{3}$-$\frac{x+4}{2}$≥-2(并用数轴表示出解集)
分析 (1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(2)去分母、去括号、移项、合并同类项、系数化成1即可求解.
解答 解:(1)$\left\{\begin{array}{l}{\frac{1+2x}{3}>x-1…①}\\{4(x-1)<3x-4…②}\end{array}\right.$,
解①得x<4,
解②得x<0.
则不等式组的解集是x<0;
(2)去分母,得2(1-2x)-3(x+4)≥-12,
去括号,得2-4x-3x-12≥-12,
移项,得-4x-3x≥-12+12-2,
合并同类项,得-7x≥-2,
系数化成1得x≤$\frac{2}{7}$. .
.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 三角形三条高都在三角形内 | |
| B. | 三角形的角平分线是射线 | |
| C. | 三角形的三条角平分线可能在三角形内,也可能在三角形外 | |
| D. | 三角形三条中线相交于一点 |
5.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
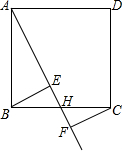 如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.