题目内容
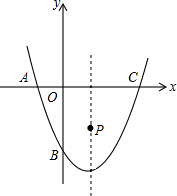 如图,抛物线y=x2-2x-3与x轴交于A,C两点,与y轴交与点B,点P是抛物线对称轴上的一个动点,若使△ABP的周长最小,则点P的坐标为
如图,抛物线y=x2-2x-3与x轴交于A,C两点,与y轴交与点B,点P是抛物线对称轴上的一个动点,若使△ABP的周长最小,则点P的坐标为考点:轴对称-最短路线问题,二次函数的性质
专题:
分析:连接BC,则BC与对称轴的交点P,此时△ABP的周长最小,求出直线BC的解析式后,可得出点P的坐标.
解答: 解:令y=0,则 x2-2x-3=0,解得x1=3,x2=-1,令x=0,则y=-3,
解:令y=0,则 x2-2x-3=0,解得x1=3,x2=-1,令x=0,则y=-3,
∴A(-1,0),C(3,0),B(0,-3),
由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点P的位置,
设直线BC解析式为y=kx+b,把B(0,-3),C(3,0)代入得:
,
解得:
,
则直线BC的解析式为y=x-3,
∵抛物线y=x2-2x-3的对称轴x=-
=-
=1
把x=1代入y=x-3得y=-2,
故点P的坐标为:(-1,2).
故答案为(-1,2).
 解:令y=0,则 x2-2x-3=0,解得x1=3,x2=-1,令x=0,则y=-3,
解:令y=0,则 x2-2x-3=0,解得x1=3,x2=-1,令x=0,则y=-3,∴A(-1,0),C(3,0),B(0,-3),
由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点P的位置,
设直线BC解析式为y=kx+b,把B(0,-3),C(3,0)代入得:
|
解得:
|
则直线BC的解析式为y=x-3,
∵抛物线y=x2-2x-3的对称轴x=-
| b |
| 2a |
| -2 |
| 2 |
把x=1代入y=x-3得y=-2,
故点P的坐标为:(-1,2).
故答案为(-1,2).
点评:本题考查了二次函数的综合运用,涉及了顶点坐标的求解、三角形的面积及轴对称求最短路径的知识,解答本题的关键是熟练各个知识点,注意培养自己解综合题的能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知A是五次多项式,B是四次多项式,则A-B的次数是( )
| A、1 | B、5 | C、4 | D、无法确定 |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )| A、②④ | B、②③④ |
| C、①②④ | D、①④ |
计算
=( )
| 2011×2012×2013×2014+1 |
| A、4050155 |
| B、4050145 |
| C、4050125 |
| D、4050115 |
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )A、
| ||||
B、4-
| ||||
C、1-
| ||||
| D、4 |
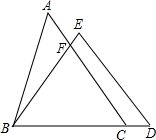 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证:
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证: 如图,点A在双曲线y=
如图,点A在双曲线y=