题目内容
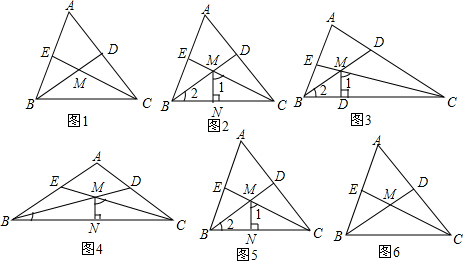
 如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )| A、110° | B、125° |
| C、130° | D、155° |
考点:全等三角形的判定与性质
专题:
分析:先证明△BCE≌△ACD,得出∠B=∠A,∠E=∠D,再根据四边形内角和定理即可求出∠BPD的度数.
解答:解:在△BCE和△ACD中,
∴△BCE≌△ACD(SSS)
∴∠A=∠B,∠D=∠E,∠ACD=∠BCE,
∴∠ACB=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠ACB=∠ECD=50°,
∴∠ACD=55°+50°=105°,
∴∠A+∠D=180°-105°=75°,
∴∠B+∠D=∠A+∠D=75°,
∴∠BPD=360°-75°-155°=130°.
|
∴△BCE≌△ACD(SSS)
∴∠A=∠B,∠D=∠E,∠ACD=∠BCE,
∴∠ACB=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠ACB=∠ECD=50°,
∴∠ACD=55°+50°=105°,
∴∠A+∠D=180°-105°=75°,
∴∠B+∠D=∠A+∠D=75°,
∴∠BPD=360°-75°-155°=130°.
点评:本题考查了全等三角形的判定与性质以及三角形内角和、四边形内角和定理,证明三角形全等是关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
计算
=( )
| 2011×2012×2013×2014+1 |
| A、4050155 |
| B、4050145 |
| C、4050125 |
| D、4050115 |
下列各方程中,哪些是一元一次方程?( )
①4x-3=x;②3x(x-2)=1;③1-2a=2a+1;④3a2=5;⑤
=3x-2;⑥x+1=
;⑦2x-6y=3x-1;⑧x=1.
①4x-3=x;②3x(x-2)=1;③1-2a=2a+1;④3a2=5;⑤
| 2x+4 |
| 3 |
| 1 |
| x |
| A、①③ | B、①③⑤ |
| C、⑤⑥ | D、①③⑤⑧ |
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )A、
| ||||
B、4-
| ||||
C、1-
| ||||
| D、4 |
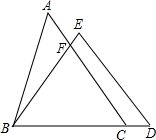 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证:
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证: