题目内容
已知:在平面直角坐标系xOy中,给出如下定义:线段AB及点P,任取AB上一点Q,线段PQ长度的最小值称为点P到线段AB的距离,记作d(P→AB).
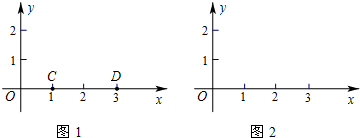
(1)如图1,已知C点的坐标为(1,0),D点的坐标为(3,0),求点P(2,1)到线段CD的距离d(P→CD)为 ;
(2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为
,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.
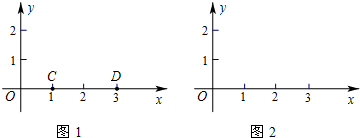
(1)如图1,已知C点的坐标为(1,0),D点的坐标为(3,0),求点P(2,1)到线段CD的距离d(P→CD)为
(2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为
| 2 |
考点:一次函数综合题
专题:
分析:(1)根据点到线段的距离的定义即可直接写出结果;
(2)分G在OE的上边和下边,两种情况进行讨论,求得直线OE中当x=1时点K的纵坐标,然后利用勾股定理求得G到K的距离,即可求得G的纵坐标.
(2)分G在OE的上边和下边,两种情况进行讨论,求得直线OE中当x=1时点K的纵坐标,然后利用勾股定理求得G到K的距离,即可求得G的纵坐标.
解答: 解:(1)d(P→CD)为 1.
解:(1)d(P→CD)为 1.
(2)在坐标平面内作出线段DE:y=x(0≤x≤3).
∵点G的横坐标为1,
∴点G在直线x=1上,设直线x=1交x轴于点H,交DE于点K,
①如图2所示,过点G1作G1F⊥DE于点F,则G1F就是点G1到线段DE的距离,
∵线段DE:y=x(0≤x≤3),
∴△G1FK,△DHK均为等腰直角三角形,
∵G1F=
∴KF=
由勾股定理得G1K=2,
又∵KH=OH=1,
∴HG1=3,即G1的纵坐标为3;
②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,
∵OH=1,
∴G2O=
∴点G2同样是满足条件的点,
∴点G2的纵坐标为-1,
综上,点G的纵坐标为3或-1.
 解:(1)d(P→CD)为 1.
解:(1)d(P→CD)为 1.(2)在坐标平面内作出线段DE:y=x(0≤x≤3).
∵点G的横坐标为1,
∴点G在直线x=1上,设直线x=1交x轴于点H,交DE于点K,
①如图2所示,过点G1作G1F⊥DE于点F,则G1F就是点G1到线段DE的距离,
∵线段DE:y=x(0≤x≤3),
∴△G1FK,△DHK均为等腰直角三角形,
∵G1F=
| 2 |
∴KF=
| 2 |
由勾股定理得G1K=2,
又∵KH=OH=1,
∴HG1=3,即G1的纵坐标为3;
②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,
∵OH=1,
∴G2O=
| 2 |
∴点G2同样是满足条件的点,
∴点G2的纵坐标为-1,
综上,点G的纵坐标为3或-1.
点评:本题考查了一次函数与勾股定理的综合应用,正确进行讨论,注意到△OHG为等腰直角三角形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是( )
| A、m≥0 | ||||
B、m≥
| ||||
C、m≤
| ||||
D、0≤m≤
|
下列真命题中逆命题也是真命题的是( )
| A、对顶角相等 |
| B、全等三角形对应角相等 |
| C、全等三角形对应边相等 |
| D、等边三角形是锐角三角形 |
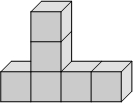 如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
如图是由一些棱长都为1cm的小正方体组合成的简单几何体.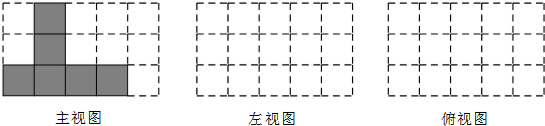

 已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.
已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.