题目内容
8.先化简,再求值:(1)(2x+3y)2-(2x+3y)(2x-3y),其中x=3,y=-1
(2)$({\frac{{{x^2}-4x+4}}{{{x^2}-4}}-\frac{x}{x+2}})÷\frac{x-1}{x+2}$,在-2,-1,1,2中选一个合适的数作为x的值.
分析 (1)利用将完全平方式展开、合并同类项等手段将原等式进行化简,再将x=3,y=-1代入化简后的算式中,算出结果即可;
(2)利用完全平方式、合并同类项等手段将原等式进行化简,根据分式成立的条件,找出x的取值范围,由此得出x的值,将其代入化简后的算式中,算出结果即可.
解答 解:(1)原式=4x2+12xy+9y2-(4x2-9y2),
=4x2+12xy+9y2-4x2+9y2,
=12xy+18y2.
当x=3,y=-1时,
原式=12×3×(-1)+18×(-1)2,
=-36+18,
=-18.
(2)原式=[$\frac{(x-2)^{2}}{(x+2)(x-2)}$-$\frac{x}{x+2}$]$•\frac{x+2}{x-1}$,
=[$\frac{x-2}{x+2}$-$\frac{x}{x+2}$]$•\frac{x+2}{x-1}$,
=$\frac{-2}{x+2}•\frac{x+2}{x-1}$,
=$\frac{2}{1-x}$.
∵(x2-4)(x+2)(x-1)≠0,
∴x≠±2,x≠1.
当x=-1时,
原式=$\frac{2}{1-(-1)}$=1.
点评 本题考查了分式的化简求值以及整式的化简求值,解题的关键是:(1)将整式进行化简;(2)确定x的数值.本题属于基础题,难度不大,解决该题型题目时,先化简再求值是关键(要注意分式成立的条件).

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
18.小华上周每天的睡眠时间为(单位:小时):7,8,10,11,8,8,9.这组数据的众数是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
19.若分式$\frac{|x|-2}{{x}^{2}-4x+4}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 2或3 |
13.-$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
17.函数y=$\frac{x}{x+2}$中,自变量x的取值范围是( )
| A. | x>-2 | B. | x≠0 | C. | x>-2且x≠0 | D. | x≠-2 |
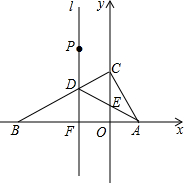 如图,平面直角坐标系中,$A(\sqrt{3},0),B({-3\sqrt{3},0}),C(0,3)$,l是AB的垂直平分线交BC于D,交x轴于F,连接AD交y轴于E,P为l上D点上一点,且DP=DE,将△DCE绕E逆时针旋转后,边CE交线段DC于M,边DE交线段DF于N,连接PM,若PM=3DN,则点N的坐标为(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$).
如图,平面直角坐标系中,$A(\sqrt{3},0),B({-3\sqrt{3},0}),C(0,3)$,l是AB的垂直平分线交BC于D,交x轴于F,连接AD交y轴于E,P为l上D点上一点,且DP=DE,将△DCE绕E逆时针旋转后,边CE交线段DC于M,边DE交线段DF于N,连接PM,若PM=3DN,则点N的坐标为(-$\sqrt{3}$,$\frac{17-\sqrt{33}}{8}$). 如图,一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m),B(3,n)两点.
如图,一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m),B(3,n)两点. 在图中建立适当的直角坐标系表示图中各景点位置.
在图中建立适当的直角坐标系表示图中各景点位置.