题目内容
3. 如图,一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m),B(3,n)两点.
如图,一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m),B(3,n)两点.(1)求一次函数及反比例函数的解析式;
(2)点P为双曲线上A,B之间的一点,求当△ABP的面积最大时点P的坐标.
分析 (1)把A、B坐标代入一次函数、反比例函数解析式列出方程组即可解决.
(2)根据对称性点P就是直线y=x与y=$\frac{3}{x}$的交点.
解答 解:(1)由题意$\left\{\begin{array}{l}{-1+b=m}\\{-3+b=n}\\{m=3n}\end{array}\right.$解得$\left\{\begin{array}{l}{b=4}\\{m=3}\\{n=1}\end{array}\right.$,
∴点A(1,3),k=3,
∴一次函数为y=-X+4,反比例函数为y=$\frac{3}{x}$.
(2)∵直线y=-x+4与反比例函数y=$\frac{3}{x}$的图象都是关于直线y=x对称的,
∴当点P是直线y=x与y=$\frac{3}{x}$的交点时,△PAB面积最大.
由$\left\{\begin{array}{l}{y=x}\\{y=\frac{3}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-\sqrt{3}}\end{array}\right.$,
∵点P在第一象限,
∴点P坐标为($\sqrt{3}$,$\sqrt{3}$).
点评 本题考查反比例函数与一次函数的交点,解题的关键是利用待定系数法,把问题转化为方程解决,根据对称性,第二个问题求点P坐标转化为求直线y=x与y=$\frac{3}{x}$的交点,属于中考常考题型.

练习册系列答案
相关题目
14.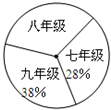 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
请你根据图表中的信息,解答下列问题:
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | b |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | a | 0.25 |
| 表(1) 其它 | 144 | 0.06 |
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
11.式子$\sqrt{x+3}$有意义的条件是( )
| A. | x≥3 | B. | x>3 | C. | x≥-3 | D. | x>-3 |
15.下列各对数中,数值相等的数是( )
| A. | 32与23 | B. | -32与(-3)2 | C. | (3×2)3与3×23 | D. | -23与(-2)3 |
13.要时分式$\frac{{x}^{2}-4}{x+2}$有意义,则x应满足的条件为( )
| A. | x≠2 | B. | x≠0 | C. | x≠±2 | D. | x≠-2 |
 如图,在8×8网格纸中,每个小正方形的边长都为1.
如图,在8×8网格纸中,每个小正方形的边长都为1.