题目内容
有三位学生参加两项不同的竞赛,则每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加的概率为 .
考点:列表法与树状图法
专题:
分析:首先用A、B分别表示两项不同的竞赛,然后画树状图,由树状图求得所有等可能的结果与每项竞赛只许有一位学生参加的情况,再利用概率公式即可求得答案.
解答:解:用A、B分别表示两项不同的竞赛,
画树状图得:

∵共有8种等可能的结果,每项竞赛只许有一位学生参加的6种情况,
∴每项竞赛只许有一位学生参加的概率为:
=
.
故答案为:
.
画树状图得:

∵共有8种等可能的结果,每项竞赛只许有一位学生参加的6种情况,
∴每项竞赛只许有一位学生参加的概率为:
| 6 |
| 8 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A、开口向下 |
| B、对称轴是x=-1 |
| C、顶点坐标是(1,2) |
| D、与x轴有两个交点 |
下列式子从左到右是因式分解的是( )
| A、(x+y)(x-y)=x2-y2 |
| B、x2-2x+3=x(x-2)+3 |
| C、a(x+y)=ax+ay |
| D、a2+2ab+b2=(a+b)2 |
 如图,A、B、C是圆O上的三个点,若∠AOC=100°,则∠ABC的度数等于( )
如图,A、B、C是圆O上的三个点,若∠AOC=100°,则∠ABC的度数等于( )| A、80° | B、130° |
| C、200° | D、150° |
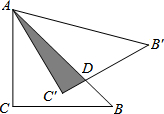 如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6
如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6 在数轴上表示下列各数,并用“<”连接起来.-3.5,-(-2),(-2)2,
在数轴上表示下列各数,并用“<”连接起来.-3.5,-(-2),(-2)2,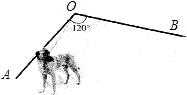 如图,墙OA、OB的夹角∠AOB=120°,一根3m长的绳子一端拴在墙角O处,另一端拴着一只小狗,求小狗可活动的区域的面积.(结果保留π)
如图,墙OA、OB的夹角∠AOB=120°,一根3m长的绳子一端拴在墙角O处,另一端拴着一只小狗,求小狗可活动的区域的面积.(结果保留π)
 如图,已知BC=EF,∠ABC=∠DEF.
如图,已知BC=EF,∠ABC=∠DEF.