题目内容
探索与思考,察下列等式:

(1)请写出第5个等式: ;
(2)根据上述规律:13+23+33+43+…+n3= .(用含n的代数式表示)
(3)利用规律计算:113+123+133+143+…+203.

(1)请写出第5个等式:
(2)根据上述规律:13+23+33+43+…+n3=
(3)利用规律计算:113+123+133+143+…+203.
考点:规律型:数字的变化类
专题:
分析:(1)(2)观察已知的等式,发现:等式的左边是连续自然数的立方和,等式的右边是连续自然数的和的平方;由此得出答案即可;
(3)根据(2)中发现的结论,即可求得13+23+33+…+203=(1+2+3+…+20)2,13+23+33+…+103=(1+2+3+…+10)2,进而求解.
(3)根据(2)中发现的结论,即可求得13+23+33+…+203=(1+2+3+…+20)2,13+23+33+…+103=(1+2+3+…+10)2,进而求解.
解答:解:(1)13+23+33+43+53=(1+2+3+4+5)2或=152;
(2)13+23+33+43+…+n3=(1+2+3+4+…+n)2或=[
]2;
(3)113+123+133+143+…+203
=(13+23+33+…+203)-(13+23+33+…+103)
=(1+2+3+…+20)2-(1+2+3+…+10)2
=2102-552
=41075.
(2)13+23+33+43+…+n3=(1+2+3+4+…+n)2或=[
| n(n+1) |
| 2 |
(3)113+123+133+143+…+203
=(13+23+33+…+203)-(13+23+33+…+103)
=(1+2+3+…+20)2-(1+2+3+…+10)2
=2102-552
=41075.
点评:此题考查数字的变化规律,找出数字的变化规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形.上述结论中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列图象不能表示y是x的函数的是( )
A、 |
B、 |
C、 |
D、 |
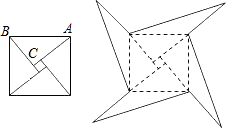 如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是
如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是 如图所示,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
如图所示,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?