题目内容
5. 要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)
要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)参考数据:$\sqrt{2}$≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
分析 过B点作BD⊥AC于D.分别在Rt△ADB和Rt△CDB中,用BD表示出AD和CD,再根据AC=AD+CD=24m列方程求出BD的值,进而求解即可.
解答 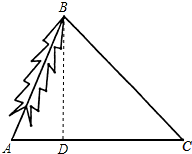 解:过B点作BD⊥AC于D.
解:过B点作BD⊥AC于D.
∵∠ACB=45°,∠BAC=66.5°,
∴在Rt△ADB中,AD=$\frac{BD}{tan66.5°}$,
在Rt△CDB中,CD=BD,
∵AC=AD+CD=24m,
∴$\frac{BD}{tan66.5°}$+BD=24,
解得BD≈16.73m.
BC=$\sqrt{2}$BD≈24m.
故支架BC的长度约为24m.
点评 本题考查解三角形的应用,解题的关键是作出辅助线构造直角三角形,利用三角函数求三角形的边.

练习册系列答案
相关题目
20. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | 2 |
 如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)①.①越来越长,②越来越短,③长度不变.
如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)①.①越来越长,②越来越短,③长度不变.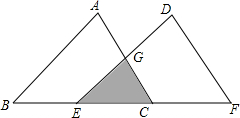 如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离.
如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离.