题目内容
20. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | 2 |
分析 连接AC、CF,根据正方形的性质得到∠ACF=90°,根据勾股定理求出AF的长,根据直角三角形中,斜边上的中线等于斜边的一半计算即可.
解答 解: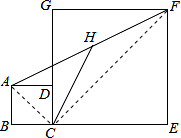 连接AC、CF,
连接AC、CF,
在正方形ABCD和正方形CEFG中,
∠ACG=45°,∠FCG=45°,
∴∠ACF=90°,
∵BC=2,CE=4,
∴AC=2$\sqrt{2}$,CF=4$\sqrt{2}$,
由勾股定理得,AF=2$\sqrt{10}$,又H是AF的中点,
∴CH=$\frac{1}{2}$AF=$\sqrt{10}$,
故选:A.
点评 本题考查的是直角三角形的性质、勾股定理的应用、正方形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
11.如果△ABC的∠A:∠B:∠C=1:2:3,CD⊥AB于点D,若AB=a,则DB=( )
| A. | a | B. | $\frac{1}{2}$a | C. | $\frac{1}{4}$a | D. | 2a |
9.某政府部门招聘公务员1人,对前来应聘的A,B,C三人进行了三项测试.他们的各项测试成绩如下表所示:
根据三项测试的平均成绩确定录用人选,那么谁将被录用?
测试项目 | 测试成绩 | ||
| A | B | C | |
| 笔 试 | 90 | 80 | 75 |
| 面 试 | 85 | 85 | 85 |
| 群众评议 | 77 | 84 | 80 |
10.在Rt△ABC中,∠C=90°,a=5,b=12,则cosA的值为( )
| A. | $\frac{12}{13}$ | B. | $\frac{12}{17}$ | C. | $\frac{5}{13}$ | D. | $\frac{5}{17}$ |
 要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)
要对一棵倾斜的古杉树AB进行保护,BC是暂时用来支撑的支架.需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求支架BC的长度.(结果取整数)