题目内容
17．
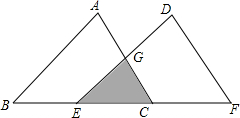如图，将△ABC沿AB方向平移得到△DEF，△ABC与△DEF重叠部分（图中阴影部分）的面积是△ABC的$\frac{1}{3}$．已知BC=3，求△ABC平移的距离．
分析 移动的距离可以视为FC或BE的长度，根据题意可知△ABC与阴影部分为相似三角形，且面积比为3：1，所以BC：EC=$\sqrt{3}$：1，推出EC=$\sqrt{3}$，所以BE=3-$\sqrt{3}$，从而求解．
解答 解：∵△ABC沿AB边平移到△DEF的位置，
∴AC∥DF，
∴△ABC∽△DBG，
∴$\frac{{S}_{阴影面积}}{{S}_{△ABC}}=（\frac{EC}{BC}）^{2}=\frac{1}{3}$，
∴BC：EC=$\sqrt{3}$：1，
∵BC=3，
∴EC=$\sqrt{3}$，
∴△ABC平移的距离为3-$\sqrt{3}$．
点评 本题主要考查相似三角形的判定和性质、平移的性质，关键在于求证△ABC与阴影部分为相似三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
要对一棵倾斜的古杉树AB进行保护，BC是暂时用来支撑的支架．需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求支架BC的长度．（结果取整数）
2．鞋厂生产不同号码的鞋，其中，生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的（ ）
| A． | 平均数 | B． | 众数 | C． | 中位数 | D． | 众数或中位数 |
9．某政府部门招聘公务员1人，对前来应聘的A，B，C三人进行了三项测试．他们的各项测试成绩如下表所示：
根据三项测试的平均成绩确定录用人选，那么谁将被录用？
测试项目 | 测试成绩 | ||
| A | B | C | |
| 笔 试 | 90 | 80 | 75 |
| 面 试 | 85 | 85 | 85 |
| 群众评议 | 77 | 84 | 80 |
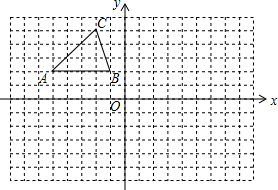在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（-1，2）．