题目内容
2．如果$\frac{a}{2x+3y}$+$\frac{b}{2x-3y}$=$\frac{4x}{4{x}^{2}-9{y}^{2}}$，那么a=1，b=1．分析 根据分式的性质，可得同分母分式，根据分式相等，可得关于a、b的方程，根据解方程，可得答案．
解答 解：分式等价于$\frac{2ax-3ay}{（2x+3y）（2x-3y）}$+$\frac{2bx+3by}{（2x+3y）（2x-3y）}$=$\frac{4x}{4{x}^{2}-9{y}^{2}}$，
$\left\{\begin{array}{l}{2a+2b=4}\\{3b-3a=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$．
故答案为：1，1．
点评 本题考查了分式的加减，通分化成同分母分式得出关于a、b的方程组是解题关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
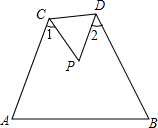如图，△ABP沿CD折叠，求证：∠1+∠2=2∠P．
如图，ABCD是四根木条钉成的四边形，为了使它不变形，小明加了根木条AE，小明的做法正确吗？说说你的理由．