题目内容
20. 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,其中乙蜡烛燃烧时y与x之间的函数关系式是y=-10x+25.
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,其中乙蜡烛燃烧时y与x之间的函数关系式是y=-10x+25.(1)甲蜡烛燃烧前的高度是30厘米,乙蜡烛燃烧的时间是25小时.
(2)求甲蜡烛燃烧时y与x之间的函数关系式.
(3)求出图中交点M的坐标,并说明点M的实际意义.
分析 (1)由图象可知:甲、乙两根蜡烛燃烧前的高度分别是30cm、25cm,从点燃到燃尽所用的时间分别是2h、2.5h;
(2)根据直线经过点的坐标列方程组解答即可;
(3)两直线的交点就是高度相同的时刻.
解答 解:(1)根据图象可得甲的长度是30cm.
y=-10x+25中令x=0,则y=25.
故答案是:30,25;
(2)设甲蜡烛燃烧时y与x之间的函数关系式为y=kx+b,
由图可知,函数的图象过点(2,0),(0,30),
∴$\left\{\begin{array}{l}{2k+b=0}\\{b=30}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-15}\\{b=30}\end{array}\right.$
∴y=-15x+30
(3)由题意得-15x+30=-10x+25,解得x=1
则M的坐标是:(1,15).
表示燃烧1小时时,甲、乙两根蜡烛的剩余高度相等,都是15厘米.
点评 本题重点考查了一次函数的图象及一次函数的应用,是一道难度中等的题目.

练习册系列答案
相关题目
5.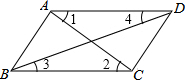 如图,下列四组条件中,能判定AB∥CD的是( )
如图,下列四组条件中,能判定AB∥CD的是( )
 如图,下列四组条件中,能判定AB∥CD的是( )
如图,下列四组条件中,能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠BAD+∠ADC=180° | C. | ∠3=∠4 | D. | ∠BAD+∠ABC=180° |
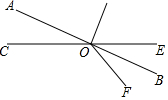 如图所示,直线AB、CE交于O,
如图所示,直线AB、CE交于O,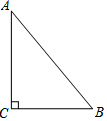 如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.