题目内容
17.观察下列各式:$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$=1$\frac{1}{2}$;$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{3}$=1$\frac{1}{6}$;
$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{4}$=1$\frac{1}{12}$,…
请你根据以上三个等式提供的信息解答下列问题
①猜想:$\sqrt{1+\frac{1}{{7}^{2}}+\frac{1}{{8}^{2}}}$=1+$\frac{1}{7}$-$\frac{1}{8}$=1$\frac{1}{56}$;
②归纳:根据你的观察,猜想,请写出一个用n(n为正整数)表示的等式:$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{{n}^{2}+n+1}{{n}^{2}+n}$;
③应用:计算$\sqrt{\frac{82}{81}+\frac{1}{100}}$.
分析 ①直接利用利用已知条件才想得出答案;
②直接利用已知条件规律用n(n为正整数)表示的等式即可;
③利用发现的规律将原式变形得出答案.
解答 解:①猜想:$\sqrt{1+\frac{1}{{7}^{2}}+\frac{1}{{8}^{2}}}$=1+$\frac{1}{7}$-$\frac{1}{8}$=1$\frac{1}{56}$;
故答案为:1+$\frac{1}{7}$-$\frac{1}{8}$,1$\frac{1}{56}$;
②归纳:根据你的观察,猜想,写出一个用n(n为正整数)表示的等式:
$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{{n}^{2}+n+1}{{n}^{2}+n}$;
③应用:$\sqrt{\frac{82}{81}+\frac{1}{100}}$
=$\sqrt{1+\frac{1}{81}+\frac{1}{100}}$
=$\sqrt{1+\frac{1}{{9}^{2}}+\frac{1}{1{0}^{2}}}$
=1+$\frac{1}{9}$-$\frac{1}{10}$
=1$\frac{1}{90}$.
点评 此题主要考查了二次根式的性质与化简,正确发现数字变化规律是解题关键.

练习册系列答案
相关题目
18.对于反比例函数y=$\frac{1}{x}$,下列说法正确的是( )
| A. | 图象经过(1,-1) | B. | 图象位于二、四象限 | ||
| C. | 图象是中心对称图形 | D. | y随x的增大而减小 |
8.与不等式$\frac{x-3}{2}$<$\frac{2x+1}{3}$-1有相同解集的不等式是( )
| A. | 3x-3<(4x+1)-1 | B. | 3(x-3)<2(2x+1)-1 | C. | 2(x-3)<3(2x+1)-6 | D. | 3x-9<4x-4 |
5.(2x)n-81分解因式后得(4x2+9)(2x+3)(2x-3),则n等于( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
12.某运动员在东西走向的公路上练习跑步,跑步情况记录如下:(向东为正,单位:米)1400,-1200,1100,-800,1000,该运动员共跑路程( )
| A. | 1500m | B. | 4500m | C. | 3700m | D. | 5500m |
2.若多项式x2+ax+b分解因式的结果(x-2)(x+3),则a,b的值分别是( )
| A. | a=1,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=5,b=-6 |
9. 已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )
已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )
 已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )
已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )| A. | abc<0 | B. | a+b<0 | C. | |c|<|a| | D. | -|c-a|=c-a |
6.下列说法正确的是( )
| A. | 一个有理数不是正数就是负数 | |
| B. | 0是绝对值最小的实数 | |
| C. | 平方根等于本身的数是0和1 | |
| D. | 数轴上位于原点两侧的数互为相反数 |
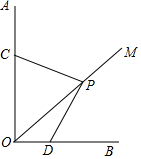 已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.
已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.