题目内容
7.已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,且皆有31项.若a2+b30=29,a30+b2=-9,则此两等差级数的和相加的结果为多少?( )| A. | 300 | B. | 310 | C. | 600 | D. | 620 |
分析 根据已知条件得到a1+b31+b1+a31=29-9,a3+b29+a29+b3=29-9,…,于是得到a1+a2+…+a30+a31+b1+b2+…+b30+b31=(a2+b30+a30+b2)+(a1+b31+b1+a31)+…+(a16+b16)=15×(29-9)+$\frac{29-9}{2}$=310.
解答 解:∵a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,
∵a2+b30=29,a30+b2=-9,
∴a1+b31+b1+a31=29-9,a3+b29+a29+b3=29-9,…,
∴a1+a2+…+a30+a31+b1+b2+…+b30+b31=(a2+b30+a30+b2)+(a1+b31+b1+a31)+…+(a16+b16)=15×(29-9)+$\frac{29-9}{2}$=310.
故选B.
点评 本题考查了数字的变化类,找出规律是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.据统计,截止2016年3月全国微信注册用户总数已达到943000000人,943000000用科学记数法可表示为( )
| A. | 9.43×104 | B. | 943×106 | C. | 9.43×106 | D. | 9.43×108 |
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5). 如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)
如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)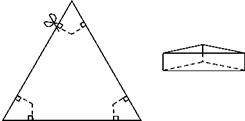 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.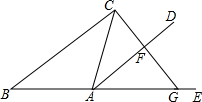 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.