题目内容
16.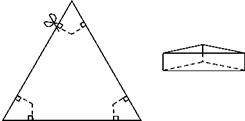 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
分析 由题意得出△ABC为等边三角形,△OPQ为等边三角形,得出∠A=∠B=∠C=60°,AB=BC=AC.∠POQ=60°,连结AO,作QM⊥OP于M,在Rt△AOD中,∠OAD=∠OAK=30°,得出OD的长,求出OP,无盖柱形盒子的容积=底面积×高,即可得出结果.
解答 解:如图由题意得:△ABC为等边三角形,△OPQ为等边三角形,AD=AK=BE=BF=CG=CH=4cm,
∴∠A=∠B=∠C=60°,AB=BC=AC,∠POQ=60°,
∴∠ADO=∠AKO=90°.
连结AO,作QM⊥OP于M,
在Rt△AOD中,∠OAD=∠OAK=30°,
∴OD=$\frac{\sqrt{3}}{3}$AD=$\frac{4\sqrt{3}}{3}$cm,
∵PQ=OP=DE=20-2×4=12(cm),
∴QM=OP•sin60°=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$(cm),
∴无盖柱形盒子的容积=$\frac{1}{2}$×12×6$\sqrt{3}$×$\frac{4\sqrt{3}}{3}$=144(cm3);
故答案为:144.
点评 本题考查了等边三角形的性质的运用,勾股定理、三角函数等知识;熟练掌握等边三角形的性质,求出等边△OPQ的边长和高是解决问题的关键.

练习册系列答案
相关题目
6.下列说法不正确的是( )
| A. | “某射击运动员射击一次,正中把靶心”属于随机事件 | |
| B. | “13名同学至少有两名同学的出生月份相同”属于必然事件 | |
| C. | “在标准大气压下,当温度降到-5℃时,水结成冰”属于随机事件 | |
| D. | “某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件 |
7.已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,且皆有31项.若a2+b30=29,a30+b2=-9,则此两等差级数的和相加的结果为多少?( )
| A. | 300 | B. | 310 | C. | 600 | D. | 620 |
11.某大学生对新一代无人机的续航时间进行7次测试,一次性飞行时间(单位:分钟)分别为20、22、21、26、25、22、25.则这7次测试续航时间的中位数是( )
| A. | 22或25 | B. | 25 | C. | 22 | D. | 21 |
1. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |


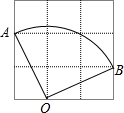 如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.