题目内容
19. 如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)
如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)
分析 延长MB交正西方向于C,根据题意先求出MB的值和AC=BC,设AC=BC=x,在Rt△ACM中,根据∠ACM=90°,得出tan∠MAC=$\frac{MC}{AC}$,求出x的值,再根据MA=2AC,求出MA,
最后根据缉私船的速度V=$\frac{MA}{2}$,即可得出答案.
解答  解:延长MB交正西方向于C,由题意可知:
解:延长MB交正西方向于C,由题意可知:
MB=2×10=20(海里),∠MAC=60°,∠1=45°,
则AC=BC.
设AC=BC=x﹒在Rt△ACM中,
∵∠ACM=90°,
∴tan∠MAC=$\frac{MC}{AC}$,即$\frac{20+x}{x}$=$\sqrt{3}$,
∴x=10($\sqrt{3}$+1),即AC=10$\sqrt{3}$+10.
又∵MA=2AC,
∴MA=20$\sqrt{3}$+20,
∴缉私船的速度为V=$\frac{MA}{2}$=10$\sqrt{3}$+10(海里/时).
点评 此题考查的知识点是解直角三角形的应用,关键是根据题意作出辅助线,构造两直角三角形,运用三角函数求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,且皆有31项.若a2+b30=29,a30+b2=-9,则此两等差级数的和相加的结果为多少?( )
| A. | 300 | B. | 310 | C. | 600 | D. | 620 |
 如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )
如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )



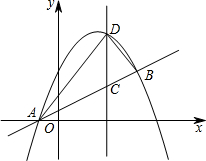 如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
如图,抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
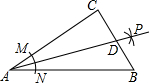 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )