题目内容
15.下列各式能用平方差公式计算的是( )| A. | (2a+b)(2b-a) | B. | (-$\frac{1}{2}$x+1)(-$\frac{1}{2}$x-1) | C. | (a+b)( a-2b) | D. | (2 x-1)(-2 x+1) |
分析 根据平方差公式即可求出答案.
解答 解:(-$\frac{1}{2}$x+1)(-$\frac{1}{2}$x-1)=(-$\frac{1}{2}$x)2-1=$\frac{1}{4}$x2-1
故选(B)
点评 本题考查平方差公式,解题的关键是熟练运用平方差公式,本题属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.用-a表示的数一定是( )
| A. | 负数 | B. | 正数或负数 | C. | 负整数 | D. | 以上全不对 |
6.若直线y=ax+b不经过第三象限,则下列不等式中,总成立的是( )
| A. | b>0 | B. | b-a<0 | C. | b-a>0 | D. | a+b>0 |
3. 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )
 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )| A. |  | B. |  | C. |  | D. |  |
7.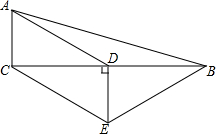 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2$\sqrt{13}$;
④四边形ACEB的面积是16.
则以上结论正确的个数是( )
 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2$\sqrt{13}$;
④四边形ACEB的面积是16.
则以上结论正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图表示的是不等式组( )的解集.
如图表示的是不等式组( )的解集.
 如图表示的是不等式组( )的解集.
如图表示的是不等式组( )的解集.| A. | $\left\{\begin{array}{l}{x≤1}\\{x<-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤1}\\{x>-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥1}\\{x<-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≥1}\\{x>-2}\end{array}\right.$ |