题目内容
(1)2x-1=x+3
(2)3x-2=-5(x+2)
(3)2x+3(2x-1)=16-(x+1)
(4)
-
=1
(5)
=
-1
(6)
=
x-2.
(2)3x-2=-5(x+2)
(3)2x+3(2x-1)=16-(x+1)
(4)
| x-3 |
| 2 |
| 4x+1 |
| 5 |
(5)
| 2(x+1) |
| 3 |
| 5(x+1) |
| 6 |
(6)
| 2x-1 |
| 4 |
| 2 |
| 3 |
考点:解一元一次方程
专题:
分析:(1)根据移项、合并同类项、化系数为1,可得方程的解.
(2)根据去括号、移项、合并同类项、化系数为1,可得方程的解.
(3)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解.
(4)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解;
(5)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解;
(6)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解.
(2)根据去括号、移项、合并同类项、化系数为1,可得方程的解.
(3)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解.
(4)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解;
(5)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解;
(6)根据去分母、去括号、移项、合并同类项、化系数为1,可得方程的解.
解答:解:(1)移项,得2x-x=3+1.
合并同类项,得x=4;
(2)去括号,得3x-2=-5x-10,
移项,得3x+5x=-10+2,
合并同类项,得8x=-8,
系数化为1,得x=-1;
(3)去括号,得2x+6x-3=16-x-1,
移项,得2x+6x+x=16-1+3,
合并同类项,得9x=18,
系数化为1,得x=2;
(4)去分母,得5(x-3)-2(4x+1)=10,
去括号,得5x-15-8x-2=10,
移项,得5x-8x=10+2+15,
合并同类项,得-3x=17,
系数化为1,得x=-
;
(5)去分母,得4(x+1)=5(x+1)-6,
去括号,得4x+4=5x+5-6,
移项,得4x-5x=5-6-4,
合并同类项,得-x=-5,
系数化为1,得x=5;
(6)去分母,得3(2x-1)=8x-24,
去括号,得6x-3=8x-24,
移项,得6x-8x=-24+3,
合并同类项,得-2x=-21
系数化为1,得x=
.
合并同类项,得x=4;
(2)去括号,得3x-2=-5x-10,
移项,得3x+5x=-10+2,
合并同类项,得8x=-8,
系数化为1,得x=-1;
(3)去括号,得2x+6x-3=16-x-1,
移项,得2x+6x+x=16-1+3,
合并同类项,得9x=18,
系数化为1,得x=2;
(4)去分母,得5(x-3)-2(4x+1)=10,
去括号,得5x-15-8x-2=10,
移项,得5x-8x=10+2+15,
合并同类项,得-3x=17,
系数化为1,得x=-
| 17 |
| 3 |
(5)去分母,得4(x+1)=5(x+1)-6,
去括号,得4x+4=5x+5-6,
移项,得4x-5x=5-6-4,
合并同类项,得-x=-5,
系数化为1,得x=5;
(6)去分母,得3(2x-1)=8x-24,
去括号,得6x-3=8x-24,
移项,得6x-8x=-24+3,
合并同类项,得-2x=-21
系数化为1,得x=
| 21 |
| 2 |
点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
下列说法中正确的是( )
| A、和同一条直线都相交的两条直线互相平行 |
| B、数轴上的点都表示的是有理数 |
| C、相等的角是对顶角 |
| D、直线l外一点A与直线l上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线l的距离是3cm |
用形状、大小完全相等的下列图形不能进行密铺的是( )
| A、等腰三角形 | B、平行四边形 |
| C、正五边形 | D、正六边形 |
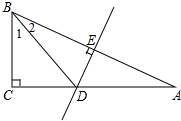 如图所示,在△ABC中,∠C=90°,AB的垂直平分线交AC于D点,垂足为E,且∠1=2∠2,求∠A的度数.
如图所示,在△ABC中,∠C=90°,AB的垂直平分线交AC于D点,垂足为E,且∠1=2∠2,求∠A的度数. 解方程组
解方程组