题目内容
4.2016年3月22日式第24个“世界水日”,校学生会主席小明同学就“节水方式”的了解程度对本校九年级学生进行了一次随机问卷调查,如图是他采集数据后绘制的两幅不完整的统计图(A:了解较多,B:不了解,C:了解一点,D:非常了解).请你根据图中提供的信息解答以下问题:
(1)在扇形统计图中的横线上填写缺失的数据,并把条形统计图补充完整.
(2)2016年该初中九年级共有学生400人,按此调查,可以估计2016年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人?
(3)在问卷调查中,选择“A”的是1名男生,1名女生,选择“D”的有有2男2女.校学生会要从选择“A、D”的问卷中,分别抽一名学生参加活动,请你用列表法或树状图求出恰好是一名男生一名女生的概率.
分析 (1)根据题意确定出样本的容量,进而求出选B与D的人数,求出各自占的百分比,补全扇形与条形统计图即可;
(2)由“了解较多”与“非常了解”的百分比,乘以400即可得到结果;
(3)列出得出所有等可能的情况数,找出恰好是一名男生一名女生的情况数,即可求出所求概率.
解答 解:(1)由条形统计图中A对应的数据和扇形统计图中A对应的百分比可知,抽取的样本容量为2÷10%=20,
故选B的有20×30%=6(人),选D的有20-2-6-8=4(人),选C的百分比为8÷20=0.4=40%;选D的百分比为4÷20=0.2=20%;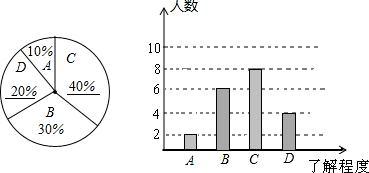
(2)∵选项“了解较多”以上的学生占抽取样本容量的(2+4)÷20=0.3=30%,
∴九年级学生中节水方式“了解较多”以上的学生约有400×30%=120人;
(3)选A的是一男一女,记作男1,女1,根据题意可知选择D的有4人且2男2女,分别记作男2,男3,女2,女3,列表如下:
| 男2 | 男3 | 女2 | 女3 | |
| 男1 | (男1,男2) | (男1,男3) | (男1,女2) | (男1,女3) |
| 女1 | (女1,男2) | (女1,男3) | (女1,女2) | (女1,女3) |
则选择1男1女的概率P=$\frac{4}{8}$=$\frac{1}{2}$.
点评 此题考查了列表法与树状图法,用样本估计总体,条形统计图,以及扇形统计图,弄清题中的数据是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
| A. | (-2,-1) | B. | (-1,0) | C. | (-1,-1) | D. | (-2,0) |
19.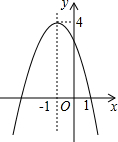 如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
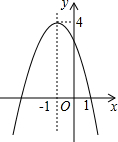 如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )
如图是二次函数:y=ax2+bx+c(a≠0)的图象,下列说法错误的是( )| A. | 函数y的最大值是4 | B. | 函效的图象关于直线x=-1对称 | ||
| C. | 当x<-1时,y随x的增大而增大 | D. | 当-4<x<1时,函数值y>0 |
 如图,AE是正八边形ABCDEFGH的一条对角线,则∠BAE=67.5°.
如图,AE是正八边形ABCDEFGH的一条对角线,则∠BAE=67.5°.