题目内容
13.某市的育中考采取抽签决定考试项目,有甲、乙、丙三人分别擅长A:游泳;B:50米;C:1000米(假设就这三个项目研究).(1)求学生甲能抽到自己的喜欢的项目的概率;
(2)如果甲乙丙三人在抽签时箱内只有个A、B、C不同项目的签,且各自抽签后将考签交给监考老师,求三人至少有一人抽到自己擅长项目的概率.
分析 (1)根据概率的定义即可解决.
(2)此题需要三步完成;因为有三名学生选择餐厅,可以看做需三次完成的事件,所以需要采用树状图法.
解答 解:(1)∵只有A、B、C三个项目,
∴学生甲能抽到自己的喜欢的项目A的概率=$\frac{1}{3}$.
(2)画树状图得,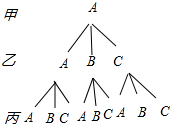
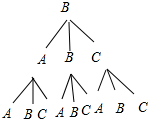
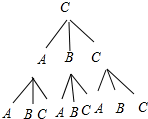
所以三人至少有一人抽到自己擅长项目的概率=$\frac{19}{27}$.
点评 此题考查的是用树状图法求概率.树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3.下列各组线段不能构成三角形的是( )
| A. | 3,7,8 | B. | 4,5,6 | C. | 6,8,15 | D. | 8,9,15 |
18. 如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
 如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
5.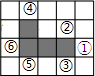 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |

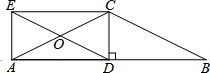 如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.