题目内容
14.已知|a|=8,b2=36,若|a-b|=b-a,求a+b的值.分析 根据绝对值和乘方的意义可得a=±8,b=±6,再由绝对值的性质可得a-b≤0,进而可确定a、b的值,然后可得答案.
解答 解:∵|a|=8,b2=36,
∴a=±8,b=±6,
∵|a-b|=b-a,
∴a-b≤0,
∴a≤b,
∴a=-8,b=-6,则a+b=-14,
a=-8,b=6,a+b=-2,
故答案为:-2或-14.
点评 此题主要考查了绝对值的性质和有理数的乘方,关键是掌握有理数乘方的意义,掌握非正数的绝对值等于它的相反数.

练习册系列答案
相关题目
4.某条抛物线向左平移1个单位,再向上平移2个单位后,所得到的方程是y=x2,那么原抛物线方程为( )
| A. | y=(x+1)2+2 | B. | y=(x+1)2-2 | C. | y=(x-1)2+2 | D. | y=(x-1)2-2 |
2.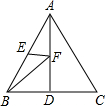 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )| A. | 7.5 | B. | 5 | C. | 4 | D. | 不能确定 |
6.对于分式$\frac{x-b}{x+a}$,当x=-1时其值为0,当x=1时此分式没有意义,那么( )
| A. | a=b=-1 | B. | a=b=1 | C. | a=1,b=-1 | D. | a=-1,b=1 |
4.$\sqrt{(-3)^{2}}$的算术平方根是( )
| A. | ±3 | B. | 3 | C. | $±\sqrt{3}$ | D. | $\sqrt{3}$ |
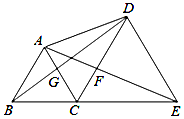 如图所示,点B、C、E在同一条直线上,AC=BC,CD=CE,∠ACB=∠DCE=60°.则下列结论:①△ACE≌△BCD;②CG=CF;③若连接GF,则GF∥BE;④△ADB≌△CEA.一定成立的有①②③.
如图所示,点B、C、E在同一条直线上,AC=BC,CD=CE,∠ACB=∠DCE=60°.则下列结论:①△ACE≌△BCD;②CG=CF;③若连接GF,则GF∥BE;④△ADB≌△CEA.一定成立的有①②③.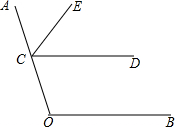 如图,点C在射线OA上,CE平分∠ACD.OF平分∠COB并与射线CD交于点F.
如图,点C在射线OA上,CE平分∠ACD.OF平分∠COB并与射线CD交于点F. 如图,已知在矩形ABCD中,AB=2a,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,△ABE是等边三角形.
如图,已知在矩形ABCD中,AB=2a,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,△ABE是等边三角形.