题目内容
设关于x的方程(a-b)3x2+(a2-3ab+2b2)x+a+b=0的根都是整数,且a-b是非零整数,求b的最小值.
考点:一元二次方程的整数根与有理根
专题:
分析:首先利用韦达定理得出a,b的关系,进而利用已知方程的根都是整数,得出符合题意的答案.
解答:解:若a-b=0,方程化为a+b=0,有无穷多个根,不合题意,
若a-b≠0,令(a-b)x=t,则t为整数,且(a-b)t2+(a-2b)t+(a+b)=0是关于t的二次方程,
由韦达定理得:
t1+t2=
,t1t2=
,
故t1t2-2(t1+t2)=3,
所以,(t1-2)(t2-2)=7,
不妨设t1≥t2,有
或
,
解得:
或
,
则
或
,
解得:13a=14b或2b=3a,
(1)若13a=14b,则a-b=
b为整数,
所以,b为整数且13|b,
又(a-b)x=t=
bx=3或9,于是,bx=39或117,
∵x是整数,b为整数且13|b,bx=39或117,
∴当x=-1时,则b最小=-117,
(2)若2b=3a,则a-b=-
b,
所以,b为整数且3|b,
又(a-b)x=t=-
bx=1或-5,于是,bx=-3或15,
∵x是整数,b为整数且3|b,bx=-3或15,
∴当x=-1时,则b最小=-15,
综上,b最小为-117.
若a-b≠0,令(a-b)x=t,则t为整数,且(a-b)t2+(a-2b)t+(a+b)=0是关于t的二次方程,
由韦达定理得:
t1+t2=
| 2b-a |
| a-b |
| a+b |
| a-b |
故t1t2-2(t1+t2)=3,
所以,(t1-2)(t2-2)=7,
不妨设t1≥t2,有
|
|
解得:
|
|
则
|
|
解得:13a=14b或2b=3a,
(1)若13a=14b,则a-b=
| 1 |
| 13 |
所以,b为整数且13|b,
又(a-b)x=t=
| 1 |
| 13 |
∵x是整数,b为整数且13|b,bx=39或117,
∴当x=-1时,则b最小=-117,
(2)若2b=3a,则a-b=-
| 1 |
| 3 |
所以,b为整数且3|b,
又(a-b)x=t=-
| 1 |
| 3 |
∵x是整数,b为整数且3|b,bx=-3或15,
∴当x=-1时,则b最小=-15,
综上,b最小为-117.
点评:此题主要考查了一元二次方程的整数根与有理根,得出a,b的关系是解题关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,已知点A(2,0),B(0,1),C(2,3),如果在第一象限内有点P(m,
如图,已知点A(2,0),B(0,1),C(2,3),如果在第一象限内有点P(m, 如图,在四边形ABCD中,AD∥BC,M为AB的中点,且DM平分∠ADC,CM平分∠BCD,AD=3cm,BC=7cm.求DC的长.
如图,在四边形ABCD中,AD∥BC,M为AB的中点,且DM平分∠ADC,CM平分∠BCD,AD=3cm,BC=7cm.求DC的长.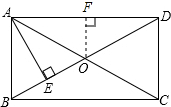 如图,矩形ABCD的对角线AC、BD相交于一点O,OF⊥AD,AE⊥BD,且BE:ED=1:3.若AC=2cm,则OF=
如图,矩形ABCD的对角线AC、BD相交于一点O,OF⊥AD,AE⊥BD,且BE:ED=1:3.若AC=2cm,则OF=