题目内容
在同一直角坐标系内画出下列二次函数图象(列表,描点,连线),观察三条抛物线的位置关系,并分别指出它们的开口方向,对称轴和顶点.
①y=
x2;
②y=
(x+2)2;
③y=
(x-2)2.
①y=
| 1 |
| 2 |
②y=
| 1 |
| 2 |
③y=
| 1 |
| 2 |
考点:二次函数的图象
专题:作图题
分析:利用列表,描点,连线画出三个函数图象,然后根据图象写出它们的开口方向,对称轴和顶点.
解答:解:列表:
 ,
,
描点:
连线,如图.

y=
x2的开口向上,对称轴为y轴,顶点坐标为(0,0);
y=
(x+2)2的开口向上,对称轴为直线x=-2,顶点坐标为(-2,0);
y=
(x-2)2的开口向上,对称轴为直线x=2,顶点坐标为(2,0).
 ,
,描点:
连线,如图.

y=
| 1 |
| 2 |
y=
| 1 |
| 2 |
y=
| 1 |
| 2 |
点评:本题考查了二次函数的图象:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,先把抛物线的解析式配成顶点式,再利用列表、描点和连线画二次函数图象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
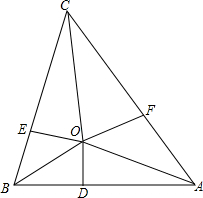 如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长.
如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长. 如图,△ABC中,D为AB中点,DE∥BC,若BC=16cm,则DE=
如图,△ABC中,D为AB中点,DE∥BC,若BC=16cm,则DE= 如图:AB长度为20厘米,AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线B自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.
如图:AB长度为20厘米,AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线B自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.