Question

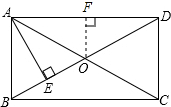如图，矩形ABCD的对角线AC、BD相交于一点O，OF⊥AD，AE⊥BD，且BE：ED=1：3．若AC=2cm，则OF=

 

cm，AE=

 

cm．

Answer 1

考点：矩形的性质

专题：计算题

分析：根据矩形的对角线相等且互相平分可得OB=OD，然后求出BE=OE，从而判断出△AOB是等边三角形，根据等边三角形的性质求出∠ABO=60°，再求出∠ADB=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得OD=2OF，再根据BD=AC=2DO即可得解．

解答：解：在矩形ABCD中，OB=OD，
∵BE：ED=1：3，
∴BE=OE，
∵AE⊥BO，
∴△AOB是等边三角形，
∴∠ABO=60°，
∴∠ADB=90°-60°=30°，
∵OF⊥AD，
∴OF=

1

2

OD=

1

4

AC=

1

4

×2=

1

2

cm，
∵OA=OD，OF⊥AD，
∴AF=DF，
∴AB=2OF=

1

2

×2=1cm，
∵BE=

1

4

BD=

1

4

AC=

1

4

×2=

1

2

cm，
∴AE=

AB2-BE2

=

12-( 1 2 )2

=

3

2

．

点评：本题考查了矩形的性质，等边三角形的判定与性质，直角三角形30°角所对的直角边等于斜边的一半，熟记性质并判断出等边三角形然后求出∠ADB=30°是解题的关键．