题目内容
11.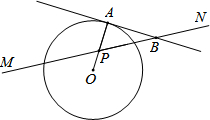 如图,⊙O的半径为2,点P是半径OA上的一个动点,过点P作直线MN且∠APN=60°,过点A的切线AB交MN于点B.设OP=x,△PAB的面积为 y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,⊙O的半径为2,点P是半径OA上的一个动点,过点P作直线MN且∠APN=60°,过点A的切线AB交MN于点B.设OP=x,△PAB的面积为 y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. |  | B. | 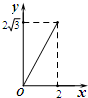 | C. |  | D. | 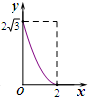 |
分析 根据已知得出S与x之间的函数关系式,进而得出函数是二次函数,当x=-$\frac{b}{2a}$=2时,S取到最小值为:$\frac{4ac-{b}^{2}}{4a}$=0,即可得出图象.
解答 解:∵A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,
∴AO=2,OP=x,则AP=2-x,
∴tan60°=$\frac{AB}{PA}$=$\sqrt{3}$,
解得:AB=$\sqrt{3}$(2-x)=-$\sqrt{3}$x+2$\sqrt{3}$,
∴S△ABP=$\frac{1}{2}$×PA×AB=$\frac{1}{2}$(2-x)•$\sqrt{3}$•(-x+2)=$\frac{\sqrt{3}}{2}$x2-2$\sqrt{3}$x+2$\sqrt{3}$,
故此函数为二次函数,
∵a=$\frac{\sqrt{3}}{2}$>0,
∴当x=-$\frac{b}{2a}$=2时,S取到最小值为:$\frac{4ac-{b}^{2}}{4a}$=0,
根据图象得出只有D符合要求.
故选:D.
点评 此题主要考查了动点函数的图象,根据已知得出S与x之间的函数解析式是解题关键.

练习册系列答案
相关题目
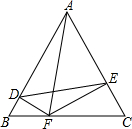 △ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,
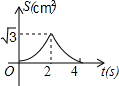
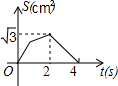
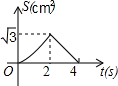
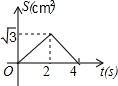
△ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,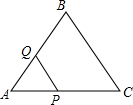 如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )
如图,在等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以1cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )