题目内容
10.阅读下文,寻找规律:已知x≠1,观察下列各式:(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4…
(1)填空:(1-x)(1+x+x2+x3+x4+x5+x6+x7)=1-x8.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=1-xn+1.
②(x-1)(x10+x9+…+x+1)=x11-1.
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25)=-63.
②1+2+22+23+24+…+22013=22014-1.
分析 (1)仿照上面等式确定出所求即可;
(2)归纳总结得到一般性规律,计算即可得到结果’
(3)根据得出的规律将原式变形,计算即可得到结果.
解答 解:(1)根据题意得:(1-x)(1+x+x2+x3+x4+x5+x6+x7)=1-x8;
(2)①(1-x)(1+x+x2+…+xn)=1-xn+1;
②(x-1)(x10+x9+…+x+1)=-(1-x11)=x11-1;
(3)①原式=1-26=1-64=-63;
②原式=-(1-2)(1+2+22+23+24+…+22013)=-(1-22014)=22014-1.
故答案为:(1)1+x+x2+x3+x4+x5+x6+x7;(2)①1-xn+1;②x11-1;(3)①-63;②22014-1.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确的是( )
| A. | -2是-4的平方根 | B. | -2是(-2)2的算术平方根 | ||
| C. | (-2)2的平方根是-2 | D. | -2是4的平方根 |
5.下列解方程正确的是( )
| A. | 由4x-6=2x+3移项得4x+2x=3-6 | |
| B. | 由$\frac{4}{7}x=5-\frac{x-1}{7}$,去分母得4x=5-x-1 | |
| C. | 由2(x+3)-3(x-1)=7,去括号得 2x+3-3x+1=7 | |
| D. | 由$\frac{x}{0.3}-0.5=x$得 $\frac{10x}{3}-\frac{1}{2}=x$ |
19.下列说法中错误的是( )
| A. | 9的算术平方根是3 | B. | 4的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
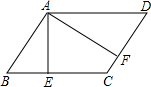 如图,已知平行四边形ABCD的周长是80cm,BC=24cm,AE=12cm
如图,已知平行四边形ABCD的周长是80cm,BC=24cm,AE=12cm 如图,已知正方形ABCD的边长为1,E为CD的中点,P为正方形ABCD边上的动点,动点P从点A出发,沿A→B→C→E运动,若点P经过的路程为x,△APE的面积为y.
如图,已知正方形ABCD的边长为1,E为CD的中点,P为正方形ABCD边上的动点,动点P从点A出发,沿A→B→C→E运动,若点P经过的路程为x,△APE的面积为y.