题目内容
20. 如图,已知正方形ABCD的边长为1,E为CD的中点,P为正方形ABCD边上的动点,动点P从点A出发,沿A→B→C→E运动,若点P经过的路程为x,△APE的面积为y.
如图,已知正方形ABCD的边长为1,E为CD的中点,P为正方形ABCD边上的动点,动点P从点A出发,沿A→B→C→E运动,若点P经过的路程为x,△APE的面积为y.(1)求y与x之间的函数关系式.
(2)当点P运动路程为多少时,△APE的面积为$\frac{1}{3}$.
分析 (1)分别从0≤x≤1,1<x≤2,2<x≤2.5去分析求解即可求得答案;
(2)分别从0≤x≤1,1<x≤2,2<x≤2.5时,y=$\frac{1}{3}$,去求解即可求得答案.
解答 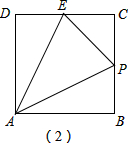 解:(1)①当0≤x≤1时,AP=x,AD=1,则y=$\frac{1}{2}$×x×1=$\frac{1}{2}$x;
解:(1)①当0≤x≤1时,AP=x,AD=1,则y=$\frac{1}{2}$×x×1=$\frac{1}{2}$x;
②如图(2),当1<x≤2时,BP=x-1,CP=2-x,
∴y=S梯形ABCE-S△ABP-S△CPE=$\frac{1}{2}$×($\frac{1}{2}$+1)×1-$\frac{1}{2}$×1×(x-1)-$\frac{1}{2}$×$\frac{1}{2}$×(2-x)=$\frac{3}{4}$-$\frac{1}{4}$x;
③如图(3),当2<x≤2.5时,EP=2.5-x,
∴y=$\frac{1}{2}$×(2.5-x)×1=$\frac{5}{4}$-$\frac{1}{2}$x;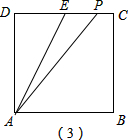 (2)①当0≤x≤1时,$\frac{1}{2}$x=$\frac{1}{3}$,
(2)①当0≤x≤1时,$\frac{1}{2}$x=$\frac{1}{3}$,
解得:x=$\frac{2}{3}$;
②当1<x≤2时,$\frac{3}{4}$-$\frac{1}{4}$x=$\frac{1}{3}$,
解得:x=$\frac{5}{3}$;
③当2<x≤2.5时,$\frac{5}{4}$-$\frac{1}{2}$x=$\frac{1}{3}$,
解得:x=$\frac{11}{6}$(舍去);
综上:当点P运动路程为$\frac{2}{3}$或$\frac{5}{3}$时,△APE的面积为$\frac{1}{3}$.
点评 此题考查了正方形的性质以及三角形的面积问题.注意分类讨论思想的应用是解此题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
8.下列说法正确的是( )
| A. | 同位角相等 | B. | 同旁内角相等 | C. | 内错角相等 | D. | 对顶角相等 |
15.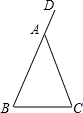 如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )
如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )
 如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )
如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )| A. | 以A点为圆心,以AD长为半径画弧,交AC与点E;再分别以D,E为圆心,再以适当长度为半径画弧,使两弧交于点P;连接AP,则AP为所求直线 | |
| B. | 取AC中点E(作法略),作射线BE,再以E点为圆心,以BE长为半径画弧,交射线BE于另一点P;连接AP,则AP为所求直线 | |
| C. | 作∠B的角平分线(作法略)BM,再以以A点为圆心,以AB长为半径画弧,交射线BM于点P,连接AP,则AP为所求直线 | |
| D. | 将BC向上平移m个单位,让m等于A点到BC的距离,则平移后的线段为所求 |
12.下列运算中正确的是( )
| A. | a5÷b-5=a5b5 | B. | a6•a4=a24 | C. | a4+b4=(a+b)4 | D. | (x3)3=x6 |

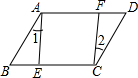 如图,平行四边形ABCD中,E,F分别是边BC,AD上的点,有下列条件:
如图,平行四边形ABCD中,E,F分别是边BC,AD上的点,有下列条件: