题目内容
2.已知x-y=$\sqrt{2}$,z-y=-$\sqrt{2}$,求x2+y2+z2-xy-yz-xz的值.分析 先求得(x+y)(z-y)的值,然后求得(x-y)-(z-y)可得到x-z=2$\sqrt{2}$,然后两个平方,最后将(x+y)(z-y)的值与(x-z)2相加即可.
解答 解:由x-y=$\sqrt{2}$,z-y=-$\sqrt{2}$得:(x+y)(z-y)=xz-xy-yz+y2=-2①;
(x-y)-(z-y)=x-z=2$\sqrt{2}$,则x2-2xz+z2=8②,
①+②得:x2+y2+z2-xy-yz-xz=-2+8=6.
点评 本题主要考查的是二次根式的化简求值,能够利用二次根式的性质进行变形是解题的关键.

练习册系列答案
相关题目
12.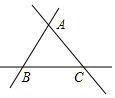 如图有三条笔直的公路AB、AC、BC两两相交围成一个三角形的建筑工地.若现在要在建筑工地外建一个沙石周转站,使周转站到三条公路的距离相等,则周转站可供选择的位置有( )个.
如图有三条笔直的公路AB、AC、BC两两相交围成一个三角形的建筑工地.若现在要在建筑工地外建一个沙石周转站,使周转站到三条公路的距离相等,则周转站可供选择的位置有( )个.
 如图有三条笔直的公路AB、AC、BC两两相交围成一个三角形的建筑工地.若现在要在建筑工地外建一个沙石周转站,使周转站到三条公路的距离相等,则周转站可供选择的位置有( )个.
如图有三条笔直的公路AB、AC、BC两两相交围成一个三角形的建筑工地.若现在要在建筑工地外建一个沙石周转站,使周转站到三条公路的距离相等,则周转站可供选择的位置有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.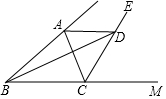 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )| A. | m-a>b-n | B. | m-a<b-n | ||
| C. | m-a=b-n | D. | m-a>b-n或m-a<b-n |

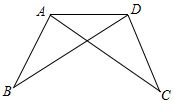 如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.
如图,AB=DC,若证明△ABD≌△DCA,可以补充的一个条件是∠BAD=∠CDA.