题目内容
10.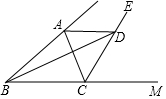 如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )
如图,△ABC中,CE平分∠ACB的外角,D为CE上一点,若BC=a,AC=b,DB=m,AD=n,则m-a与b-n的大小关系是( )| A. | m-a>b-n | B. | m-a<b-n | ||
| C. | m-a=b-n | D. | m-a>b-n或m-a<b-n |
分析 在CM上截取CG=CA,连接DG.只要证明△ACD≌△GCD,在△BDG中,利用三边关系即可解决问题.
解答 解:在CM上截取CG=CA,连接DG.
∵CD=CD,∠ACD=∠DCG,AC=CG,
∴△ACD≌△GCD,
∴AD=DG=n,
在△BDG中,BD=m,BG=BC+CG=BC+AC=a+b,
∴m+n>a+b,
∴m-a>b-n.
故选A.
点评 本题考查全等三角形的性质与判定、三角形三边的关系.解决本题的关键是恰当添加辅助线,将BC、AC、DB、AD间的关系转化为三角形三边关系.

练习册系列答案
相关题目
15.若a<0,b>0,化简|b-a+1|+|a-b-5|的结果为( )
| A. | 4 | B. | -2a+2b+6 | C. | -4 | D. | 不能确定 |
20.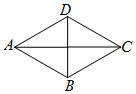 如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )
如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )
 如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )
如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )| A. | 20 | B. | 25 | C. | $\frac{25\sqrt{3}}{2}$ | D. | 25$\sqrt{3}$ |
 如图,在△ABC中,AB=AC,CM平分∠ACB,与AB交于点M,AD⊥BC于点D,ME⊥BC于点E,MF⊥MC与BC交于点F,求证:CF=4DE.
如图,在△ABC中,AB=AC,CM平分∠ACB,与AB交于点M,AD⊥BC于点D,ME⊥BC于点E,MF⊥MC与BC交于点F,求证:CF=4DE.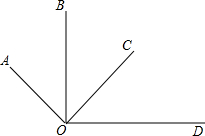 如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC中,正确的有①③④(填序号).
如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC中,正确的有①③④(填序号).