题目内容
10.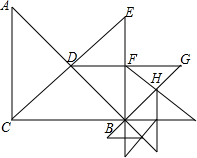 如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,CD⊥AB,垂足为D,以BD为一条直角边向三角形外作第二个等腰Rt△BDE,再以BF为一条直角边向三角形外作第三个等腰Rt△BFG,如此下去,如果Rt△ABC的斜边为记为c1,论上述方法所作的等腰直角三角形的斜边依次记为c2、c3、c4、…、cn,则c2015=$\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,CD⊥AB,垂足为D,以BD为一条直角边向三角形外作第二个等腰Rt△BDE,再以BF为一条直角边向三角形外作第三个等腰Rt△BFG,如此下去,如果Rt△ABC的斜边为记为c1,论上述方法所作的等腰直角三角形的斜边依次记为c2、c3、c4、…、cn,则c2015=$\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.
分析 根据等腰直角三角形的斜边和直角边的关系可得AB=$\sqrt{2}$BC=2,然后根据等腰直角三角形的性质得出BD=$\frac{1}{2}$AB=1,进而求得BE=$\sqrt{2}$BD=$\sqrt{2}$,同理可得被分成的第三个…第n个等边三角形斜边,即可求得等2015个等腰直角三角形的斜边.
解答 解:∵在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,
∴c1=2,
∵CD⊥AB,垂足为D,以BD为一条直角边向三角形外作第二个等腰Rt△BDE,
c2=$\sqrt{2}$,
再以BF为一条直角边向三角形外作第三个等腰Rt△BFG,
c3=1,
如此下去,
c4=$\frac{\sqrt{2}}{2}$
…
cn=2×($\frac{\sqrt{2}}{2}$)n-1,
∴c2015=2×($\frac{\sqrt{2}}{2}$)2014=$\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.
故答案为 $\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.
点评 本题考查了等腰直角三角形斜边和直角边的关系,等腰直角三角形的性质,求出第n个等腰直角三角形斜边长是解题的关键.

练习册系列答案
相关题目
15.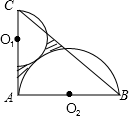 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )| A. | $\frac{46-13π}{4}$ | B. | $\frac{32-9π}{2}$ | C. | $\frac{23-13π}{4}$ | D. | $\frac{54-13π}{4}$ |
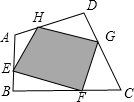 如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA上的点,且AH=$\frac{1}{3}$AD,BE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$BC,DG=$\frac{1}{3}$CD,如果阴影部分的面积为10平方厘米,则四边形ABCD的面积等于18平方厘米.
如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA上的点,且AH=$\frac{1}{3}$AD,BE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$BC,DG=$\frac{1}{3}$CD,如果阴影部分的面积为10平方厘米,则四边形ABCD的面积等于18平方厘米. 如图,已知在△ABC中,AB=6,BC=10,AC=8,D是AB的中点,DE∥BC,EF∥AB,则四边形DBFE的周长等于( )
如图,已知在△ABC中,AB=6,BC=10,AC=8,D是AB的中点,DE∥BC,EF∥AB,则四边形DBFE的周长等于( )