题目内容
通分：
，
，
．
| 1 |
| 2a2b |
| 3 |
| 4ab2 |
| 5 |
| 6ac2 |
考点：通分
专题：计算题
分析：先确定最简公分母为12a2b2c2，再把各分母分解因式，然后根据分式的基本性质把分母都化为12a2b2c2即可．
解答：解：最简公分母为12a2b2c2，
=
，
=
，
=
．
| 1 |
| 2a2b |
| 6bc2 |
| 12a2b2c2 |
| 3 |
| 4ab2 |
| 9ac2 |
| 12a2b2c2 |
| 5 |
| 6ac2 |
| 10ab2 |
| 12a2b2c2 |
点评：本题考查了通分：把几个异分母的分式分别化为与原来的分式相等的同分母的分式，这样的分式变形叫做分式的通分．通分的关键是确定最简公分母．
练习册系列答案
相关题目
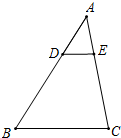在△ABC中，D和E分别在AB、AC上，且DE∥BC，AD：DB=1：2，则下列结论中正确的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的一元二次方程mx2-2x+1=0有实数根，则实数m的取值范围是（ ）
| A、m≥1 |
| B、m≤1 |
| C、m≥1且m≠0 |
| D、m≤1且m≠0 |
如图，四边形ABCD的四个顶点都在⊙O上，AC是直径，DE⊥AC，垂足为点E，DE与CB的延长线相交于点F，求证：CD2=CB•CF．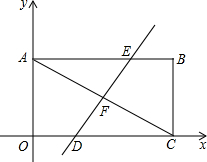
如图，平面直角坐标系中，矩形OABC的对角线AC=10，边OA=6．