题目内容
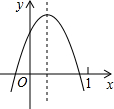 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①abc>0;②方程ax2+bx+c=0的两根之和大于0;③2a+b<0;④a-b+c<0,
其中正确的是(填序号)
考点:二次函数图象与系数的关系
专题:
分析:根据抛物线的开口方向、抛物线对称轴位置以及抛物线与y轴交点的位置确定a、b、c的符号;由根与系数的关系确定两根之和的符号;当x=-1时,根据图象找到相应的y值的符号.
解答:解:①抛物线开口方向向下,则a<0.
对称轴在y轴的右侧,则a、b异号,即b>0.
抛物线与y轴交于正半轴,则c>0.
所以 abc<0.
故①错误;
②设程ax2+bx+c=0的两根为α、β,则α+β=-
.
∵a、b异号,
∴α+β=-
>0,
即方程ax2+bx+c=0的两根之和大于0.
故②正确;
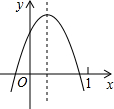
③∵对称轴在y轴的右侧,
∴1>-
>0,
又∵a<0,
∴-b>2a
∴2a+b<0.
故③正确.
④如图,当x=-1时,根据对称性得到:y>0,即a-b+c<0.
故④正确;
综上所述,正确的结论是②③④.
故答案是:②③④.
对称轴在y轴的右侧,则a、b异号,即b>0.
抛物线与y轴交于正半轴,则c>0.
所以 abc<0.
故①错误;
②设程ax2+bx+c=0的两根为α、β,则α+β=-
| b |
| a |
∵a、b异号,
∴α+β=-
| b |
| a |
即方程ax2+bx+c=0的两根之和大于0.
故②正确;
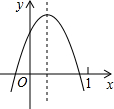
③∵对称轴在y轴的右侧,
∴1>-
| b |
| 2a |
又∵a<0,
∴-b>2a
∴2a+b<0.
故③正确.
④如图,当x=-1时,根据对称性得到:y>0,即a-b+c<0.
故④正确;
综上所述,正确的结论是②③④.
故答案是:②③④.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在(-1)3,(-1)2012,-22,(-3)2这四个数中,最大的数与最小的数的差等于( )
| A、10 | B、8 | C、5 | D、13 |
 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )| A、1 | B、2 | C、3 | D、4 |
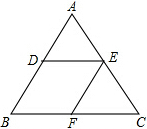 如图,D、E、F分别是△ABC的AB、AC、BC边上的点,且DE∥BC,EF∥AB.
如图,D、E、F分别是△ABC的AB、AC、BC边上的点,且DE∥BC,EF∥AB. 如图△ABC中,DE∥BC,AD=2,BD=3,BC=6,则DE=
如图△ABC中,DE∥BC,AD=2,BD=3,BC=6,则DE=