题目内容
利用函数y=
x2-
x-3的图象,借助计算器探索方程
x2-
x-3=0的介于-3与-2之间的根(精确到0.1)
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
考点:图象法求一元二次方程的近似根
专题:
分析:根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解答: 解:方程
解:方程
x2-
x-3=0的根是函数y=
x2-
x-3与x轴交点的横坐标.
作出二次函数y=
x2-
x-3的图象,如图所示,
由图象可知方程有两个根,一个在-3与-2之间,另一个在2和3之间.
求-3与-2之间的根,
当x=-2.2时,y=-0.14;
当x=-2.3时,y=0.105;
因此,x=-2.3是方程介于-3与-2之间的一个近似根.
 解:方程
解:方程| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
作出二次函数y=
| 1 |
| 2 |
| 1 |
| 5 |
由图象可知方程有两个根,一个在-3与-2之间,另一个在2和3之间.
求-3与-2之间的根,
当x=-2.2时,y=-0.14;
当x=-2.3时,y=0.105;
因此,x=-2.3是方程介于-3与-2之间的一个近似根.
点评:本题考查了图象法求一元二次方程的近似根,解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
若|m|=3,|n|=5且m-n>0,则m+n的值是( )
| A、-2 |
| B、-8或-2 |
| C、-8或 8 |
| D、8或-2 |
用一个平面分别去截:①球;②四棱柱;③圆锥;④圆柱;⑤正方体.截面可能是三角形的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
下列“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
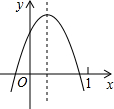 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论: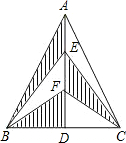 如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=
如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影= 如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=
如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=