题目内容
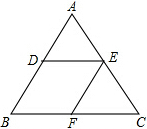 如图,D、E、F分别是△ABC的AB、AC、BC边上的点,且DE∥BC,EF∥AB.
如图,D、E、F分别是△ABC的AB、AC、BC边上的点,且DE∥BC,EF∥AB.(1)求证:△ADE∽△EFC.
(2)如果△ADE和△EFC的面积分别是16和25,求四边形BFED的面积.
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠AED=∠C,∠ADE=∠EFC,问题即可解决.
(2)首先运用相似三角形的性质求出AE:EC的值,进而求出AE:AC的值;设S四边形BFED=μ;证明△ADE∽△ABC,列出方程
=
,求出μ问题即可解决.
(2)首先运用相似三角形的性质求出AE:EC的值,进而求出AE:AC的值;设S四边形BFED=μ;证明△ADE∽△ABC,列出方程
| 16 |
| 16+25+μ |
| 16 |
| 81 |
解答: 解:(1)∵DE∥BC,EF∥AB,
解:(1)∵DE∥BC,EF∥AB,
∴∠AED=∠C,∠ADE=∠B,∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC.
(2)∵△ADE∽△EFC,
∴
=(
)2,而S△ADE=16,S△EFC=25,
∴AE:EC=4:5,设AE=4λ,则EC=5λ,AC=9λ;
则AE:AC=4λ:9λ=4:9,
设S四边形BFED=μ;
∵DE∥BC,
∴△ADE∽△ABC,
∴
=(
)2=
,
即
=
,
解得:μ=40,
即四边形BFED的面积为40.
 解:(1)∵DE∥BC,EF∥AB,
解:(1)∵DE∥BC,EF∥AB,∴∠AED=∠C,∠ADE=∠B,∠EFC=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC.
(2)∵△ADE∽△EFC,
∴
| S△ADE |
| S△EFC |
| AE |
| EC |
∴AE:EC=4:5,设AE=4λ,则EC=5λ,AC=9λ;
则AE:AC=4λ:9λ=4:9,
设S四边形BFED=μ;
∵DE∥BC,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| AE |
| AC |
| 16 |
| 81 |
即
| 16 |
| 16+25+μ |
| 16 |
| 81 |
解得:μ=40,
即四边形BFED的面积为40.
点评:考查了相似三角形的判定与性质,该题以三角形为载体,以相似三角形的判定及其性质的应用为核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用一个平面分别去截:①球;②四棱柱;③圆锥;④圆柱;⑤正方体.截面可能是三角形的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
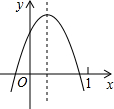 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论: 如图,幼儿园计划用20米的围栏靠墙围成一个小矩形花园ABCD.设AB=x,矩形的面积为S平方米.那么x为多少时,S的值最大?
如图,幼儿园计划用20米的围栏靠墙围成一个小矩形花园ABCD.设AB=x,矩形的面积为S平方米.那么x为多少时,S的值最大?