题目内容
6.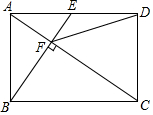 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
分析 ①正确.只要证明∠EAC=∠ACB,∠ABC=∠AFE=90°即可;
②正确.由AD∥BC,推出△AEF∽△CBF,推出AE和CF的关系即可;
③正确.只要证明DM垂直平分CF,即可证明;
④不正确.设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,求出a和b的关系,可得tan∠CAD的值.
解答 解:如图,过D作DM∥BE交AC于N,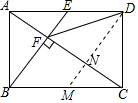 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有 $\frac{b}{a}$=$\frac{2a}{b}$,即b=$\sqrt{2}$a,
∴tan∠CAD=$\frac{DC}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$.故④不正确;
正确的有①②③,
故选B.
点评 本题主要考查了相似三角形的判定和性质,矩形的性质,图形面积的计算以及解直角三角形的综合应用,正确的作出辅助线构造平行四边形是解题的关键.解题时注意:相似三角形的对应边成比例.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案 如图,AB∥CD,∠A+∠E=80°,则∠C为( )
如图,AB∥CD,∠A+∠E=80°,则∠C为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
| A. | x•x3=x3 | B. | a3•a2=a5 | C. | x3+x6=x9 | D. | b3•b3=2b3 |
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
| 累计车费 | 0 | 0.5 | 0.9 | a | b | 1.5 |
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
 如图,P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=4.
如图,P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=4.