题目内容
14. 如图,P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=4.
如图,P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=4.
分析 根据平行四边形的对边相等可得AB=CD,AD=BC,设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,然后利用三角形的面积公式求出S1+S4=S2+S3,即可得出答案
解答 解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,
则S4=$\frac{1}{2}$ABh1,S1=$\frac{1}{2}$BCh2,S4=$\frac{1}{2}$CDh3,S1=$\frac{1}{2}$ADh4,
∵$\frac{1}{2}$ABh1+$\frac{1}{2}$CDh3=$\frac{1}{2}$AB•hAB,$\frac{1}{2}$BCh2+$\frac{1}{2}$ADh4=BC•hBC,
又∵S平行四边形ABCD=AB•hAB=BC•hBC
∴S2+S4=S1+S3,
∴S3-S2=S4-S1=6-2=4;
故答案为:4.
点评 本题考查了平行四边形的性质,三角形的面积,以及平行四边形对角线上点的判定的应用,用平行四边形的面积表示出相对的两个三角形的面积的和是解题的关键,也是本题的难点.

练习册系列答案
相关题目
4.某企业生产季节性产品,当产品无利润时,企业自动停产,经过调研,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=-n2+12n-11,则企业停产的月份为( )
| A. | 1月和11月 | B. | 1月、11月和12月 | C. | 1月 | D. | 1月至11月 |
5.在直角坐标平面内的机器人接受指令“[α,A]”(α≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向正前方沿直线行走α.若机器人的位置在原点,正前方为y轴的负半轴,则它完成一次指令[4,30°]后位置的坐标为( )
| A. | (-2,2$\sqrt{3}$) | B. | (-2,-2$\sqrt{3}$) | C. | (-2,-2) | D. | (-2,2) |
9.某种药品两次降价后,每盒从25元降到16元,则平均每次降价的百分率是( )
| A. | 10% | B. | 20% | C. | 25% | D. | 30% |
6.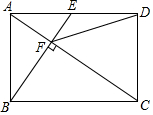 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
4.在半径为2的圆中,扇形AOB的圆心角为60°,则这个扇形的面积为( )
| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |