题目内容
6.对于任意不相等的两个数a,b,定义一种运算*如下:a*b=$\frac{2\sqrt{a+b}}{a-b}$,如3*2=$\frac{2\sqrt{3+2}}{3-2}$=2$\sqrt{5}$,那么12*4的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先依据定义列出算式,然后再进行计算即可.
解答 解:12*4=$\frac{2\sqrt{12+4}}{12-4}$=$\frac{\sqrt{16}}{4}$=$\frac{4}{4}$=1.
故选:A.
点评 本题主要考查的是算术平方根的性质,根据定义运算列出算式是解题的关键.

练习册系列答案
相关题目
14.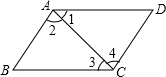 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )| A. | ∠1=∠3 | B. | ∠B+∠BCD=180° | C. | ∠2=∠4 | D. | ∠D+∠BAD=180° |
1.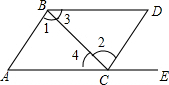 如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是( )
 如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是( )| A. | ∠1=∠2 | B. | ∠D+∠ACD=180° | C. | ∠D=∠DCE | D. | ∠3=∠4 |
15.已知a2=25,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | 2或-12 | C. | -2或12 | D. | -2或-12 |
16.在下列实数中,无理数是( )
| A. | 0 | B. | -$\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | $\sqrt{9}$ |
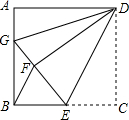 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=$\frac{72}{5}$.其中正确结论的个数是( )