题目内容
 如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为
如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为考点:切线的性质,勾股定理,垂径定理
专题:计算题,压轴题
分析:连接OC,OB,由大圆的弦AB与小圆相切,根据切线的性质得到OC垂直于AB,再由垂径定理得到C为AB的中点,由AB的长,求出BC的长,在直角三角形OBC中,根据勾股定理列出关系式,将BC的长代入求出OB2-OC2的长,由阴影部分为圆环形,根据大圆的面积减去小圆的面积可求出,表示出圆环的面积,将OB2-OC2的值代入即可求出圆环的面积,即为阴影部分的面积.
解答:解:连接OC,OB,如图所示:

∵AB与小圆相切,∴OC⊥AB,
∴C为AB的中点,又AB=10,
∴BC=AC=
AB=5,
在直角三角形OBC中,
根据勾股定理得:OB2=OC2+BC2=OC2+25,
∴OB2-OC2=25,
则图中阴影部分面积S=πOB2-πOC2=(OB2-OC2)π=25π.
故答案为:25π

∵AB与小圆相切,∴OC⊥AB,
∴C为AB的中点,又AB=10,
∴BC=AC=
| 1 |
| 2 |
在直角三角形OBC中,
根据勾股定理得:OB2=OC2+BC2=OC2+25,
∴OB2-OC2=25,
则图中阴影部分面积S=πOB2-πOC2=(OB2-OC2)π=25π.
故答案为:25π
点评:此题考查了切线的性质,勾股定理,垂径定理,以及圆环面积的求法,利用了数形结合及整体代入的思想,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
太阳的光线是( )
| A、平行的 |
| B、由一点发出的 |
| C、不平行的 |
| D、向四面八方发散的 |
 已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为
已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为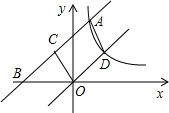 如图,直线y=x+3交反比例函数
如图,直线y=x+3交反比例函数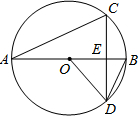 如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2
如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2