题目内容
 如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,
如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,(1)△ABP与△PCE相似吗?为什么?
(2)若AB=4,BC=7,BP=5,求CE的长.
考点:相似三角形的判定与性质
专题:
分析:(1)利用条件可证明∠APB=∠PEC,可证得结论;
(2)利用(1)中的相似得到对应边成比例,代入可求得CE.
(2)利用(1)中的相似得到对应边成比例,代入可求得CE.
解答:解:(1)相似,证明如下:
∵∠APE=∠B=60°,
∴∠BPA+∠EPC=∠EPC+∠PEC=120°,
∴∠BPA=∠PEC,且∠B=∠C,
∴△ABP∽△PCE;
(2)由(1)可知△ABP∽△PCE,
∴
=
,
∵BC=7,BP=5,
∴PC=BC-BP=7-5=2,
∴
=
,
解得CE=2.5.
∵∠APE=∠B=60°,
∴∠BPA+∠EPC=∠EPC+∠PEC=120°,
∴∠BPA=∠PEC,且∠B=∠C,
∴△ABP∽△PCE;
(2)由(1)可知△ABP∽△PCE,
∴
| AB |
| PC |
| BP |
| CE |
∵BC=7,BP=5,
∴PC=BC-BP=7-5=2,
∴
| 4 |
| 2 |
| 5 |
| CE |
解得CE=2.5.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形对应边成比例是解题的关键,注意利用三角形内角和定理找角相等.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、4是2的平方根 |
| B、2是4的算术平方根 |
| C、0的算术平方根不存在 |
| D、-1是-1的算术平方根 |
下列命题是真命题的是( )
| A、等底等高的两个三角形全等 |
| B、周长相等的直角三角形都全等 |
| C、有两边和一角对应相等的两个三角形全等 |
| D、有一边对应相等的两个等边三角形全等 |
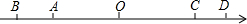
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,CE⊥AD,垂足为O,EF∥BC.求证:EC平分∠FED. 如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线.
如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线.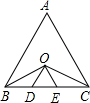 如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.
如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC. 以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么?
以A为顶点的射线个数,与直线l上的线段的条数有什么关系?为什么? 在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有多少条?
在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有多少条?