题目内容
11.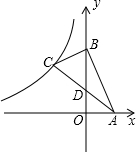 如图所示,直线y=-3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{32}{3}$.
如图所示,直线y=-3x+6交x轴、y轴于A、B两点,BC⊥AB,且D为AC的中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{32}{3}$.
分析 求出A、B坐标,根据D为斜边上的中线,得到BD=AD,设出D点坐标,表示出BD长度,即为AD长度,在Rt△AO中,求出m的值,再求出BC的解析式,AD的解析式,组成方程组,解出C点坐标,代入反比例函数解析式即可求出k的值.
解答 解:当x=0时,y=6,则B(0,6);
当y=0时,x=2,则A(2,0);
∵BC⊥AB,D为AC中点,
∴DB=AD,
设D(0,m),则AD=BD=6-m,
Rt△ABC中,22+m2=(6-m)2,
解得m=$\frac{8}{3}$,
则D(0,$\frac{8}{3}$).
∵BC⊥AB,
∴设BC解析式为y=$\frac{1}{3}$x+b,把B(0,6)代入得,b=6,函数解析式为y=$\frac{1}{3}$x+6,
设AD解析式为y=nx+a,
把A(2,0),D(0,$\frac{8}{3}$)分别代入解析式得,
$\left\{\begin{array}{l}2n+a=0\\ a=\frac{8}{3}\end{array}\right.$,
解得$\left\{\begin{array}{l}a=\frac{8}{3}\\ n=-\frac{4}{3}\end{array}\right.$,
函数解析式为y=-$\frac{4}{3}$x+$\frac{8}{3}$,
将y=$\frac{1}{3}$x+6和y=-$\frac{4}{3}$x+$\frac{8}{3}$组成方程组得,$\left\{\begin{array}{l}y=\frac{1}{3}x+6\\ y=-\frac{4}{3}x+\frac{8}{3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}x=-2\\ y=\frac{16}{3}\end{array}\right.$,
故C点坐标为(-2,$\frac{16}{3}$),
将C(-2,$\frac{16}{3}$)代入y=$\frac{k}{x}$得,k=-$\frac{32}{3}$,
故答案为-$\frac{32}{3}$.
点评 本题考查了反比例函数综合题,涉及勾股定理、待定系数法求一次函数解析式、方程组的解与函数图象交点的关系等知识,综合性强,值得关注.

 阅读快车系列答案
阅读快车系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | ±2 | B. | ±$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | 第二、三、四象限 | B. | 第一、二、三象限 | C. | 第一、三、四象限 | D. | 第一、二、四象限 |