题目内容
在Rt△AOB中,AO=6,BO=8,P为AB上一动点,PM⊥AO,以O为圆心OP为半径画⊙O.
(1)当PM2=AM•OM时,求证:AB是⊙O的切线;
(2)当P在运动的过程中,⊙O与线段AB交于另一点E,分别过P,E作AO的垂线如图所示,求PM+EN的值.
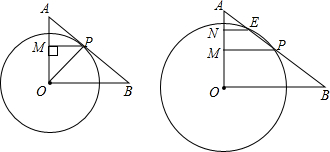
(1)当PM2=AM•OM时,求证:AB是⊙O的切线;
(2)当P在运动的过程中,⊙O与线段AB交于另一点E,分别过P,E作AO的垂线如图所示,求PM+EN的值.
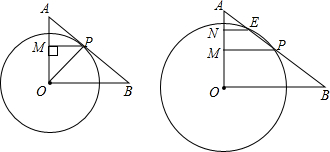
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)由PM2=AM•OM,结合∠AMP=∠OMP,可证得△AMP∽△PMO,可得∠APM=∠POM,可得到∠APM+∠OPM=90°,可知AB为⊙O的切线;
(2)过O作OQ⊥AB于Q,则Q为PE中点,过Q作QR∥OB交AO于R,则R为MN中点,可知QR为梯形MNEP的中位线,易求得AQ再由AR:AQ=AO:AB,可求得QR,从而可求得PM+EN.
(2)过O作OQ⊥AB于Q,则Q为PE中点,过Q作QR∥OB交AO于R,则R为MN中点,可知QR为梯形MNEP的中位线,易求得AQ再由AR:AQ=AO:AB,可求得QR,从而可求得PM+EN.
解答:(1)证明:∵PM⊥AO,
∴∠AMP=∠PMO,
∵PM2=AM•OM,
∴
=
,
∴△AMP∽△PMO,
∴∠APM=∠POM,
∴∠APM+∠OPM=∠POM+∠OPM=90°,
∴AB为⊙O的切线;
(2)解:如图,过O作OQ⊥AB于Q,则Q为PE中点,过Q作QR∥OB交AO于R,则R为MN中点,
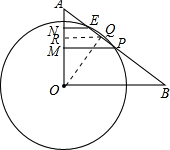
∴QR为梯形MNEP的中位线,
∴PM+NE=2QR,
又AO=6,BO=8,
∴AB=10,
∴OQ=
,
在Rt△AQO中由勾股定理可求得AQ=
,
∵QR∥OB,
∴
=
,即
=
,
解得QR=
,
∴PM+NE=
.
∴∠AMP=∠PMO,
∵PM2=AM•OM,
∴
| AM |
| PM |
| PM |
| MO |
∴△AMP∽△PMO,
∴∠APM=∠POM,
∴∠APM+∠OPM=∠POM+∠OPM=90°,
∴AB为⊙O的切线;
(2)解:如图,过O作OQ⊥AB于Q,则Q为PE中点,过Q作QR∥OB交AO于R,则R为MN中点,

∴QR为梯形MNEP的中位线,
∴PM+NE=2QR,
又AO=6,BO=8,
∴AB=10,
∴OQ=
| 24 |
| 5 |
在Rt△AQO中由勾股定理可求得AQ=
| 18 |
| 5 |
∵QR∥OB,
∴
| AQ |
| AB |
| QR |
| OB |
| ||
| 10 |
| QR |
| 8 |
解得QR=
| 72 |
| 25 |
∴PM+NE=
| 144 |
| 25 |
点评:本题主要考查切线的性质和判定及相似三角形的判定,在第(2)问中把PM+EN转化为求QR的长是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知
=
=
=k(a+b+c≠0),则k=( )
| c |
| a+b |
| b |
| a+c |
| a |
| b+c |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
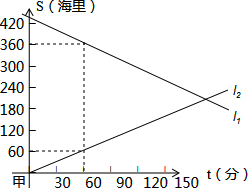 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.