题目内容
16.设a=($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$),求2004a-1的值.分析 设b=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$,a变形后,利用单项式乘以多项式,以及多项式乘以多项式法则计算,去括号合并求出a的值,代入原式计算即可得到结果.
解答 解:设b=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$,
可得a=(b-1)(b-$\frac{1}{2004}$)-b(b-1-$\frac{1}{2004}$)=b2-$\frac{1}{2004}$b-b+$\frac{1}{2004}$-b2+b+$\frac{1}{2004}$b=$\frac{1}{2004}$,
则原式=1-1=0.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.甲、乙、丙、丁四人进行射击测试,每人10次,射击成绩的平均数都是8.6环,方差分别是S甲2=0.45,S乙2=0.50,S丙2=0.55,S丁2=0.60,则射击成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
6.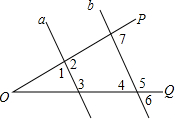 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )| A. | ∠3+∠4=180° | B. | ∠2+∠5>180° | C. | ∠1+∠6<180° | D. | ∠2+∠7=180° |